题目内容
在1和2之间插入2n个数,组成首项为1,末项为2的等差数列,若此数列前n+1项的和与末n+1项的和之比为9:13,则n= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由题意可知该等差数列的首项a1=1、a2n+2=2,求出公差d,再等差数列的前n项和和题意列出方程,求出n的值.
解答:
解:由题意可知,该等差数列的首项a1=1,a2n+2=2,
则此数列的公差d=
=
,
∵此数列前n+1项的和与末n+1项的和之比为9:13,
∴
=
,
即13[(n+1)+
×
]=9[2(n+1)-
×
],
解得,n=5,
故答案为:5.
则此数列的公差d=
| 2-1 |
| 2n+2-1 |
| 1 |
| 2n+1 |
∵此数列前n+1项的和与末n+1项的和之比为9:13,
∴
(n+1)a1+
| ||
(n+1)a2n+2+
|
| 9 |
| 13 |
即13[(n+1)+
| n(1+n) |
| 2 |
| 1 |
| 2n+1 |
| n(1+n) |
| 2 |
| 1 |
| 2n+1 |
解得,n=5,
故答案为:5.
点评:本题考查等差数列的性质和前n项和公式,注意末n+1项看成首项是2、公差是原来公差的相反数的数列,属基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
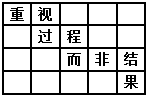 将“重视过程而非结果”8个汉字填入5*4的方格内,其中“重”字填入左上角,“果”字填入右下角,将其余6个汉字依次填入方格,要求只能向右或向下读成一句原话,如图所示为一种填法,则共有
将“重视过程而非结果”8个汉字填入5*4的方格内,其中“重”字填入左上角,“果”字填入右下角,将其余6个汉字依次填入方格,要求只能向右或向下读成一句原话,如图所示为一种填法,则共有