题目内容
11. 如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.(1)求证:平面CFM⊥平面BDF;
(2)点N在CE上,EC=2,FD=3,当CN为何值时,MN∥平面BEF.
分析 (1)推导出四边形BCDM是正方形,从而BD⊥CM,又DF⊥CM,由此能证明CM⊥平面BDF.
(2)过N作NO∥EF,交EF于O,连结MO,则四边形EFON是平行四边形,连结OE,则四边形BMON是平行四边形,由此能推导出N是CE的中点时,MN∥平面BEF.
解答  证明:(1)∵FD⊥底面ABCD,∴FD⊥AD,FD⊥BD
证明:(1)∵FD⊥底面ABCD,∴FD⊥AD,FD⊥BD
∵AF=BF,∴△ADF≌△BDF,∴AD=BD,
连接DM,则DM⊥AB,
∵AB∥CD,∠BCD=90°,
∴四边形BCDM是正方形,∴BD⊥CM,
∵DF⊥CM,∴CM⊥平面BDF.
解:(2)当CN=1,即N是CE的中点时,MN∥平面BEF.
证明如下:
过N作NO∥EF,交ED于O,连结MO,
∵EC∥FD,∴四边形EFON是平行四边形,
∵EC=2,FD=3,∴OF=1,∴OD=2,
连结OE,则OE∥DC∥MB,且OE=DC=MB,
∴四边形BMOE是平行四边形,则OM∥BE,又OM∩ON=O,
∴平面OMN∥平面BEF,
∵MN?平面OMN,∴MN∥平面BEF.
点评 本题考查线面垂直的证明,考查满足线面平行的点的位置的确定,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
19.在三角形中,角A,B,C的对边分别为a,b,c,若2sinAcosC=sinB,则$\frac{a}{c}$的值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
16.不等式|x+1|-|x-5|<4的解集为( )
| A. | (-∞,4) | B. | (-∞,-4) | C. | (4,+∞) | D. | (-4,+∞) |
3.运行如图所示的程序框图,则输出的数是7的倍数的概率为( )
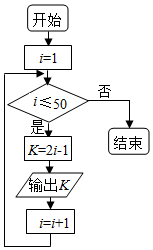

| A. | $\frac{4}{25}$ | B. | $\frac{8}{49}$ | C. | $\frac{7}{50}$ | D. | $\frac{14}{99}$ |
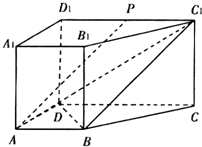 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.