题目内容
15.已知复数z满足(2-3i)z=3+2i(i是虚数单位),则z的模为1.分析 根据向量的复数运算和向量的模即可求出.
解答 解:(2-3i)z=3+2i,
∴z=$\frac{3+2i}{2-3i}$=$\frac{(3+2i)(2+3i)}{(2-3i)(2+3i)}$=$\frac{13i}{13}$=i,
∴|z|=1,
故答案为:1.
点评 本题考查了向量的复数运算和向量的模,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知函数$f(x)=2{sin^2}(x+\frac{π}{4})$,则下列结论正确的是( )
| A. | f(x)是奇函数 | B. | x=$-\frac{π}{4}$是f(x)一条对称轴 | ||
| C. | f(x)的最小正周期为$\frac{π}{2}$ | D. | ($-\frac{π}{4}$,0)是f(x)的一条对称轴 |
10.设f(x)=ax2+bx+2是定义在[1+a,1]上的偶函数,则f(x)>0的解集为( )
| A. | (-2,2) | B. | ∅ | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |
20.“$\sqrt{a}>\sqrt{b}$”是“ea>eb”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
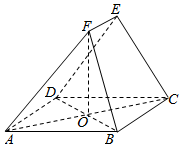 如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=60°,对角线AC与BD相交于O;OF⊥平面ABCD,BC=CE=DE=2EF=2.
如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=60°,对角线AC与BD相交于O;OF⊥平面ABCD,BC=CE=DE=2EF=2.