题目内容
10.设f(x)=ax2+bx+2是定义在[1+a,1]上的偶函数,则f(x)>0的解集为( )| A. | (-2,2) | B. | ∅ | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |
分析 根据偶函数的定义域关于原点对称便可得出a=-2,而根据f(-x)=f(x)便可以得出2bx=0,从而得出b=0,这样便得出f(x)=-2x2+2,从而解不等式-2x2+2>0便可得出f(x)>0的解集.
解答 解:f(x)为定义在[1+a,1]上的偶函数;
∴1+a=-1;
∴a=-2;
又f(-x)=f(x);
即ax2-bx+2=ax2+bx+2;
∴2bx=0;
∴b=0;
∴f(x)=-2x2+2;
∴由f(x)>0得,-2x2+2>0;
解得-1<x<1;
∴f(x)>0的解集为(-1,1).
故选:D.
点评 考查偶函数的定义,偶函数定义域的对称性,以及一元二次不等式的解法.

练习册系列答案
相关题目
1.弹簧振子的振动在简谐振动,如表给出的振子在完成一次全振动的过程中的时间t与位移y之间的对应数据,根据这些数据求出这个振子的振动的函数解析式为y=-20cos($\frac{π}{6{t}_{0}}$t).
| t | 0 | t0 | 2t0 | 3t0 | 4t0 | 5t0 | 6t0 | 7t0 | 8t0 | 9t0 | 10t0 | 11t0 | 12t0 |
| y | -20.0 | -17.8 | -10.1 | 0.1 | 10.3 | 17.1 | 20.0 | 17.7 | 10.3 | 0.1 | -10.1 | -17.8 | -20.0 |
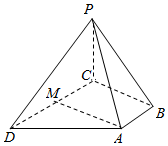 如图:四棱锥P-ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.
如图:四棱锥P-ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.