题目内容
7.若(1+x)+(1+x)2+…+(1+x)5=a0+a1(1-x)+a2•(1-x)2+…+a5(1-x)5,则a1+a2+a3+a4+a5等于( )| A. | 5 | B. | 62 | C. | -57 | D. | -56 |
分析 在所给的等式中,分别令x=1,可得a0=62;令x=0,可得a0+a1+a2+a3+a4+a5 =5,从而求得 a1+a2+a3+a4+a5 的值.
解答 解:∵(1+x)+(1+x)2+…+(1+x)5=a0+a1(1-x)+a2•(1-x)2+…+a5(1-x)5,
令x=1,可得a0=2+22+23+24+25=62,
再令x=0,可得a0+a1+a2+a3+a4+a5 =5,∴a1+a2+a3+a4+a5 =-57,
故选:C.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.已知非零平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,“|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.已知x,y满足$\left\{\begin{array}{l}x+2y-3≤0\\ x+3y-3≥0\\ y≤1\end{array}\right.$,z=2x+y的最大值为m,若正数a,b满足a+b=m,则$\frac{1}{a}+\frac{1}{b}$的最小值为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |




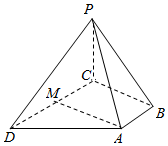 如图:四棱锥P-ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.
如图:四棱锥P-ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点. 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为f(x)=2sin($\frac{π}{3}$x+$\frac{π}{6}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为f(x)=2sin($\frac{π}{3}$x+$\frac{π}{6}$).