题目内容

求下列函数的值域
（1）y=
1-3x
；
（2）y=
x2-2x+3
；
（3）y=
1
x2+2x+3
．
考点：函数的值域
专题：计算题,配方法
分析：（1）考查被开方数大于等于0．
（2）被开方数先进行配方，再结合实数的平方非负性，即可求得．
（　　）分母配方，再求倒数的值域．
解答： 解：（1）y≥0．
（2）y=
(x-1)2+2
≥2．
（3）y=
1
(x+1)2+2
∈(0，
1
2
]．
故答案为：（1）[0，+∞）
（2）[2，+∞）
（3）(0，
1
2
]．
点评：如果涉及到二次函数，先可以考虑配方，再根据具体的式子求值域．
练习册系列答案
相关题目
给出下列命题：
①若ab＞0，a＞b，则
1
a
＜
1
b
；
②若已知直线x=m与函数f（x）=sinx，g（x）=sin（
π
2
-x）的图象分别交于点M，N，则|MN|的最大值为
2
；
③若数列an=n2+λn（λ∈N*）为单调递增数列，则λ取值范围是λ＜-2；
④若直线l的斜率k＜1，则直线l的倾斜角-
π
2
＜α＜
π
4
；
其中真命题的序号是：
 
．
下列命题中正确的是（　　）
A、若
a
∥
b
，
b
∥
c
，则
a
与
c
所在直线平行
B、向量
a
、
b
、
c
共面即它们所在直线共面
C、空间任意两个向量共面
D、若
a
∥
b
，则存在唯一的实数λ，使
a
=λ
b
若不等式2x＞x2+a对于一切x∈[-2，3]恒成立，则实数a的取值范围（　　）
A、（-∞，-8）
B、（-∞，-3）
C、（-∞，1）
D、（-8，-∞）
已知函数f（x）=
ax3-3
2x2+1
（a＞2），若在区间[1，2]上f（x）＞0恒成立，求a的取值范围．
已知函数f（x）=ex-e-x（x?R）
（Ⅰ）求证：当x≥0时，f(x)≥2x+
x3
3
；
（Ⅱ）试讨论函数H（x）=f（x）-ax（x∈R）的零点个数．
已知f（x）=x|x-a|+b，x∈R．
（1）当a=1，b=1时．f（2x）=
5
4
，求x的值；
（2）若b＜0，b为常数，任意x∈[0，1]，不等式f（x）＜0恒成立，求实数a的取值范围．
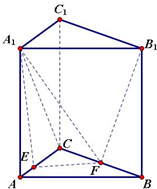如图在三棱柱ABC-A1B1C1中，各侧棱都垂直于底面且地面为等腰直角三角形，∠ACB=90°，AC=BC=4，AA1=4，E，F分别在AC，BC上，且CE=3，CF=2，求几何体EFC-A1B1C1的体积．
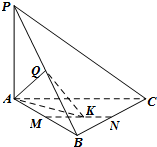如图，在三棱锥P-ABC中，直线PA⊥平面ABC，且∠ABC=90°，又点Q，M，N分别是线段PB，AB，BC的中点，且点K是线段MN上的动点．
（Ⅰ）证明：直线QK∥平面PAC；
（Ⅱ）若PA=AB=BC=8，且二面角Q-AK-M的平面角的余弦值为
3
9
，试求MK的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网