题目内容
已知|x 12-x 22+b（x1-x2）|≤4对任意x1，x2∈[-1，1]恒成立，求b的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用
分析：将不等式进行因式分解，利用绝对值不等式的性质即可求得b的取值范围．
解答：
解：|x 12-x 22+b（x1-x2）|=|（x1-x2）（x1+x2+b）|=|x1-x2|•|x1+x2+b|≤4，
∵x1，x2∈[-1，1]，
∴x1∈[-1，1]，x2∈[-1，1]，
则x1+x2∈[-2，2]，x1-x2∈[-2，2]，
即0≤|x1-x2|≤2，
要使|x1-x2|•|x1+x2+b|≤4成立，
则|x1+x2+b|≤2即可，
∵b-2≤x1+x2+b≤b+2，
∴
，
即
，
∴0≤b≤4，
即b的取值范围是[0，4]．
∵x1，x2∈[-1，1]，
∴x1∈[-1，1]，x2∈[-1，1]，
则x1+x2∈[-2，2]，x1-x2∈[-2，2]，
即0≤|x1-x2|≤2，
要使|x1-x2|•|x1+x2+b|≤4成立，
则|x1+x2+b|≤2即可，
∵b-2≤x1+x2+b≤b+2，
∴
|
即
|
∴0≤b≤4，
即b的取值范围是[0，4]．
点评：本题主要考查不等式恒成立问题，利用绝对值不等式的性质是解决本题的关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
下列命题中正确的是（ ）
A、若
| ||||||||||||
B、向量
| ||||||||||||
| C、空间任意两个向量共面 | ||||||||||||
D、若
|
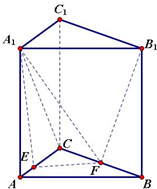如图在三棱柱ABC-A1B1C1中，各侧棱都垂直于底面且地面为等腰直角三角形，∠ACB=90°，AC=BC=4，AA1=4，E，F分别在AC，BC上，且CE=3，CF=2，求几何体EFC-A1B1C1的体积．
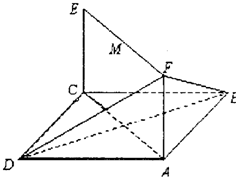已知平行四边形ABCD和矩形ACEF所在的平面互相垂直，AB=1，AD=2，∠ADC=60°，AF=a（a＞0）
在三棱锥P-ABC中，侧棱长均为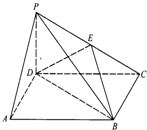
如图，四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是正方形，PD=AB=2，E为PC中点．
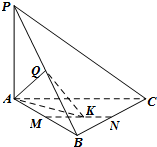如图，在三棱锥P-ABC中，直线PA⊥平面ABC，且∠ABC=90°，又点Q，M，N分别是线段PB，AB，BC的中点，且点K是线段MN上的动点．