题目内容
8.已知函数$f(x)=\frac{1}{2}a{x^2}-(a+1)x+lnx$,$g(x)={x^2}-2bx+\frac{7}{8}$.(1)当a<1时,求函数f(x)的单调区间;
(2)当$a=\frac{1}{4}$时,函数f(x)在(0,2]上的最大值为M,若存在x∈[1,2],使得g(x)≥M成立,求实数b的取值范围.
分析 (1)求出导数f′(x),分情况讨论:①a=0时,解不等式f′(x)>0,f′(x)<0即得f(x)的单调区间;②a≠0时,解方程f′(x)=0得x=1或x=$\frac{1}{a}$,按照1与$\frac{1}{a}$的大小讨论,根据f′(x)的符号即可求得其单调区间;
(2)当a=$\frac{1}{4}$时,借助(1)问单调性易求得M,存在x∈[1,2],使g(x)≥-$\frac{9}{8}$,等价于g(x)max≥-$\frac{9}{8}$,由二次函数的性质可得不等式组,解出即可.
解答 解:(1)f′(x)=ax-(a+1)+$\frac{1}{x}$=$\frac{(ax-1)(x-1)}{x}$(x>0),
①当a=0时,解f′(x)=-$\frac{x-1}{x}$>0,得0<x<1,由f′(x)<0,得x>1,
所以函数f(x)的递增区间为(0,1),递减区间为在(1,+∞);
②a≠0时,令f'(x)=0得x=1或x=$\frac{1}{a}$,
i)当0<a<1时,$\frac{1}{a}$>1,当x变化时f(x)、f′(x)随x的变化情况如下表:
| x | (0,1)) | 1 | (1,$\frac{1}{a}$) | $\frac{1}{a}$ | ($\frac{1}{a}$,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 减 | 增 |
ii)当a<0时,$\frac{1}{a}$<0,
在(0,1)上f'(x)>0,在(1,+∞)上f'(x)<0,
所以函数f(x)的递增区间为(0,1),递减区间为(1,+∞);
(2)由(1)知,当a=$\frac{1}{4}$时,f(x)在(0,1)上是增函数,在(1,2)上是减函数,
所以M=f(1)=-$\frac{9}{8}$,
存在x∈[1,2],使g(x)≥-$\frac{9}{8}$,即存在x∈[1,2],使x2-2bx+$\frac{7}{8}$≥-$\frac{9}{8}$,
只需函数g(x)在[1,2]上的最大值大于等于-$\frac{9}{8}$,
所以有 $\left\{\begin{array}{l}{g(1)≥-\frac{9}{8}}\\{g(2)≥-\frac{9}{8}}\end{array}\right.$,即 $\left\{\begin{array}{l}{1-2b+\frac{7}{8}≥-\frac{9}{8}}\\{4-4b+\frac{7}{8}≥-\frac{9}{8}}\end{array}\right.$,解得:b≤$\frac{3}{2}$,
所以b的取值范围是(-∞,$\frac{3}{2}$].
点评 本题考查利用导数研究函数的单调性、在闭区间上的最值等知识,考查分类讨论思想,考查学生分析解决问题的能力,把存在性问题转化为最值问题是解决(2)问的关键.

练习册系列答案
相关题目
16.下列关于幂函数y=xα(α∈Q)的论述中,正确的是( )
| A. | 当α=0时,幂函数的图象是一条直线 | |
| B. | 幂函数的图象都经过(0,0)和(1,1)两个点 | |
| C. | 若函数f(x)为奇函数,则f(x)在定义域内是增函数 | |
| D. | 幂函数f(x)的图象不可能在第四象限内 |
13.已知复数z=1+i,则 $\frac{{{z^2}-2z}}{1-z}$=( )
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
17.已知角α的终边经过点(m,9),且$tanα=\frac{3}{4}$,则sinα的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
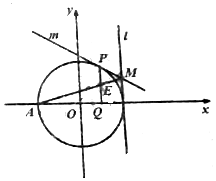 如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.
如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.