题目内容
9.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点为F,若双曲线上存在点A使△AOF为正三角形,则双曲线C的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{2}$+1 |
分析 由于OF为半焦距c,利用等边三角形性质,即可得点A的一个坐标,代入双曲线标准方程即可得双曲线的离心率.
解答 解:∵双曲线上存在点A使△AOF为正三角形,
设F为右焦点,OF=c,A在第一象限,
∴点A的坐标为($\frac{1}{2}$c,$\frac{\sqrt{3}}{2}$c)
代入双曲线方程得:$\frac{{c}^{2}}{4{a}^{2}}$-$\frac{3{c}^{2}}{4{b}^{2}}$=1,
即为$\frac{{c}^{2}}{4{a}^{2}}$-$\frac{3{c}^{2}}{4({c}^{2}-{a}^{2})}$=1,
即$\frac{1}{4}$e2-$\frac{3{e}^{2}}{4{e}^{2}-4}$=1,
解得e=1+$\sqrt{3}$.
故选:C.
点评 本题主要考查了双曲线的标准方程、双曲线的几何性质,双曲线的离心率的定义及其求法,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在△ABC中,B=45°,C=60°,c=1,则b=( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
4.某几何体的三视图如图所示,则该几何体的体积为( )
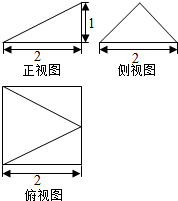

| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
1.某几何的三视图如图所示,该几何体各个面中,面积最大的是( )
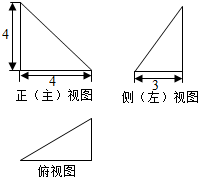

| A. | $2\sqrt{34}$ | B. | $8\sqrt{2}$ | C. | 10 | D. | $6\sqrt{2}$ |
18.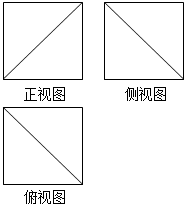 已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
 已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )| A. | 180 | B. | 144 | C. | 92 | D. | 180或144 |
19.已知⊙O1与⊙O2的半径分别为R、r,且它们是方程x2-9x+14=0的两根,若⊙O1与⊙O2相切,则圆心距O1O2等于( )
| A. | 5 | B. | 9 | C. | 5或9 | D. | 10或18 |