题目内容
17．在△ABC中，B=45°，C=60°，c=1，则b=（ ）| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{\sqrt{6}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
分析 利用正弦定理即可得出．
解答 解：由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$可得，$b=\frac{csinB}{sinC}=\frac{{1×sin{{45}°}}}{{sin{{60}°}}}=\frac{{1×\frac{{\sqrt{2}}}{2}}}{{\frac{{\sqrt{3}}}{2}}}\frac{{\sqrt{6}}}{3}$．
故选：A．
点评 本题考查了正弦定理解三角形，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
5．已知A、B是一锐角三角形两内角，直线l过P（1，0），以$\overrightarrow d=（sinB-cosA，cosB-sinA）$为其方向向量，则直线l一定不通过（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
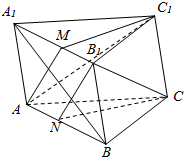如图所示，在直三棱柱ABC-A1B1C1中，BC=AC，AC1⊥A1B，M，N分别是A1B1，AB的中点，给出下列结论：①C1M⊥平面A1ABB1，②A1B⊥NB1，③平面AMC1∥平面CNB1，其中正确结论的个数为（ ）
9．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点为F，若双曲线上存在点A使△AOF为正三角形，则双曲线C的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{3}+1$ | D． | $\sqrt{2}$+1 |