题目内容
19.已知在平面直角坐标系xoy中的一个椭圆,它的中心在原点,左焦点为$F(-\sqrt{3},0)$,右顶点为D(2,0),P,Q分别是椭圆的左顶点和下顶点,过原点的直线交椭圆于A,B,且A点在第一象限,自A点作x轴的垂线,交x轴于C点,连BC.(1)求该椭圆的标准方程;
(2)若AB平分线段PQ,求直线AB的斜率kAB;并在此情况下,求A到直线BC的距离.
分析 (1)求出椭圆的半长轴a=2,半焦距$c=\sqrt{3}$,则半短轴b=1,然后求解椭圆的标准方程.
(2)求出AB的斜率kAB,得到直线AB的方程与椭圆方程$\frac{x^2}{4}+{y^2}=1$联立,求出直线BC的方程,利用点A到直线BC的距离公式求解即可.
解答 解:(1)由已知得椭圆的半长轴a=2,半焦距$c=\sqrt{3}$,则半短轴b=1
又椭圆的焦点在x轴上,∴椭圆的标准方程为$\frac{x^2}{4}+{y^2}=1$…(4分)
(2)由(1)知,P(-2,0),Q(0,-1),则PQ的中点坐标为$(-1,-\frac{1}{2})$,
若AB平分线段PQ,则AB过PQ的中点,又AB过原点,
所以AB的斜率kAB=$\frac{{-\frac{1}{2}-0}}{-1-0}=\frac{1}{2}$.…(7分)
此时直线AB的方程为$y=\frac{1}{2}x$,与椭圆方程$\frac{x^2}{4}+{y^2}=1$联立,解得$x=±\sqrt{2}$.
这样$A(\sqrt{2},\frac{{\sqrt{2}}}{2}),B(-\sqrt{2},-\frac{{\sqrt{2}}}{2}),C(\sqrt{2},0)$,所以直线BC的方程为$x-4y-\sqrt{2}=0$
故点A到直线BC的距离为$d=\frac{{|{\sqrt{2}-4×\frac{{\sqrt{2}}}{2}-\sqrt{2}}|}}{{\sqrt{{1^2}+{{(-4)}^2}}}}=\frac{{2\sqrt{34}}}{17}$…(13分)
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
14.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为45°的直线交双曲线右支于M点,若MF2垂直x轴,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
11.某几何体的三视图如图所示(其中主视图和左视图相同),则该几何体的体积为( )
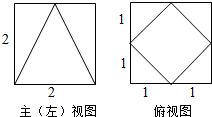

| A. | $\frac{17}{2}$ | B. | $\frac{20}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{25}{4}$ |
9.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点为F,若双曲线上存在点A使△AOF为正三角形,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{2}$+1 |
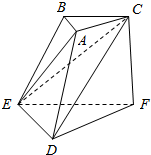 如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.