题目内容
4.某几何体的三视图如图所示,则该几何体的体积为( )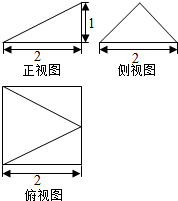
| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
分析 根据几何体的三视图,得出该几何体是底面为正方形,高为1的四棱锥,求出它的体积即可.
解答 解:根据几何体的三视图,得;
该几何体是底面为边长等于2的正方形,高为1的四棱锥;
所以该几何体的体积为
V=$\frac{1}{3}$×22×1=$\frac{4}{3}$.
故选:D.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是由三视图得出几何体的结构特征,是基础题目.

练习册系列答案
相关题目
14.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为45°的直线交双曲线右支于M点,若MF2垂直x轴,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
9.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点为F,若双曲线上存在点A使△AOF为正三角形,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{2}$+1 |
14.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=3x-1,则f(log35)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | $\frac{4}{9}$ |
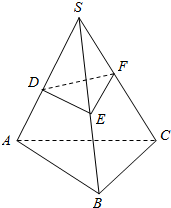 如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.
如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.