题目内容
9.设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=x${\;}^{\frac{1}{2}}$,则f(-$\frac{5}{2}$)=-$\frac{\sqrt{2}}{2}$.分析 根据函数奇偶性和周期性的关系进行转化求解即可.
解答 解:∵f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=x${\;}^{\frac{1}{2}}$,
∴f(-$\frac{5}{2}$)=f(-$\frac{5}{2}$+2)=f(-$\frac{1}{2}$)=-f($\frac{1}{2}$)=-$(\frac{1}{2})^{\frac{1}{2}}$=-$\sqrt{\frac{1}{2}}$=-$\frac{\sqrt{2}}{2}$,
故答案为:-$\frac{\sqrt{2}}{2}$
点评 本题主要考查函数值的计算,根据函数奇偶性和周期性的关系进行转化是解决本题的关键.

练习册系列答案
相关题目
19.2012年中华人民共和国环境保护部批准《环境空气质量标准》为国家环境质量标准,该标准增设和调整了颗粒物、二氧化氮、铅、笨等的浓度限值,并从2016年1月1日起在全国实施.空气质量的好坏由空气质量指数确定,空气质量指数越高,代表空气污染越严重,某市对市辖的某两个区加大了对空气质量的治理力度,从2015年11月1日起监测了100天的空气质量指数,并按照空气质量指数划分为:指标小于或等于115为通过,并引进项目投资.大于115为未通过,并进行治理.现统计如下.
(Ⅰ)以频率值作为概率值,求甲区和乙区通过监测的概率;
(Ⅱ)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元)..在(Ⅰ)的前提下,记X为通过监测,引进项目增加的税收总额,求随机变量X的分布列和数学期望.
| 空气质量指数 | (0,35] | [35,75] | (75,115] | (115,150] | (150,250] | >250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
| 乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
(Ⅱ)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元)..在(Ⅰ)的前提下,记X为通过监测,引进项目增加的税收总额,求随机变量X的分布列和数学期望.
4.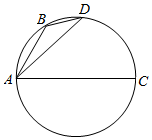 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
1.已知函数f(x)=2sin2(ωx+$\frac{π}{6}$)(ω>0)在区间[0,$\frac{π}{2}$]内单调递增,则ω的最大值是( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |