题目内容
4.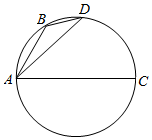 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
分析 可连接CD,CB,从而得到CD⊥AD,BC⊥AB,这便可得到$|\overrightarrow{AC}|cos∠DAC=|\overrightarrow{AD}|$,$|\overrightarrow{AC}|cos∠BAC=|\overrightarrow{AB}|$,从而得出$\overrightarrow{AC}•\overrightarrow{BD}=\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$=$|\overrightarrow{AD}{|}^{2}-|\overrightarrow{AB}{|}^{2}$,带入$AD=\sqrt{t+2},AB=\sqrt{t+1}$便可求出$\overrightarrow{AC}•\overrightarrow{BD}$的值.
解答 解:如图,连接CD,CB;
∵AC为直径;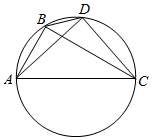
∴CD⊥AD,BC⊥AB;
∴$\overrightarrow{AC}•\overrightarrow{BD}=\overrightarrow{AC}•(\overrightarrow{AD}-\overrightarrow{AB})$
=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$
=$|\overrightarrow{AC}|cos∠DAC•|\overrightarrow{AD}|-|\overrightarrow{AC}|cos∠BAC•|\overrightarrow{AB}|$
=$|\overrightarrow{AD}{|}^{2}-|\overrightarrow{AB}{|}^{2}$
=t+2-(t+1)
=1.
故选A.
点评 考查直径所对的圆周角为直角,余弦函数的定义,以及向量减法的几何意义,向量数量积的运算及其计算公式.

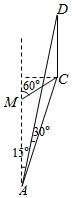 如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.
如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为600$\sqrt{2}$m.