题目内容
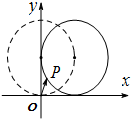 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,| OP |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:设滚动后的圆的圆心为C并设∠BCP=θ,求出⊙C的方程和参数方程,由题意求出角θ,再由三角函数的诱导公式,化简可得P为(2-sin2,1-cos2),即可求出
的坐标.
| OP |
解答:
解:设滚动后的圆的圆心为C,切点为A(2,0),连接CP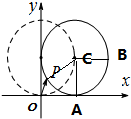
过C作与x轴正方向平行的射线,交圆C于B(2,1),设∠BCP=θ
∵⊙C的方程为(x-1)2+(y-1)2=1,
∴根据圆的参数方程,得P的坐标为(1+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(1,1)
∴∠ACP=1,可得θ=
+1,
可得cosθ=cos(
-1)=-sin1,sinθ=sin(
-1)=-cos2,
代入上面所得的式子,得到P的坐标为(1-sin2,1-cos2),
所以
的坐标是(1-sin1,1-cos1),
故答案为:(1-sin1,1-cos1).

过C作与x轴正方向平行的射线,交圆C于B(2,1),设∠BCP=θ
∵⊙C的方程为(x-1)2+(y-1)2=1,
∴根据圆的参数方程,得P的坐标为(1+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(1,1)
∴∠ACP=1,可得θ=
| 3π |
| 2 |
可得cosθ=cos(
| 3π |
| 2 |
| 3π |
| 2 |
代入上面所得的式子,得到P的坐标为(1-sin2,1-cos2),
所以
| OP |
故答案为:(1-sin1,1-cos1).
点评:本题根据半径为1的圆的滚动,求一个向量的坐标,考查了圆的参数方程和平面向量的坐标表示的应用等知识点,属于中档题.

练习册系列答案
相关题目
已知向量
=(2,1),
=(-1,k2-2),则k=2是
⊥
的( )
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“a>2”是“函数y=ax是增函数”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
某次考试结束后,从考号为1-1000号的1000份试卷中,采用系统抽样法抽取50份试卷进行试评,则在考号区间[850,949]之中被抽到的试卷份数为( )
| A、一定是5份 |
| B、可能是4份 |
| C、可能会有10份 |
| D、不能具体确定 |
已知原命题:若a+b>2,则a,b至少有一个大于1,那么原命题与其逆命题的真假情况是( )
| A、原命题真,逆命题假 |
| B、原命题假,逆命题真 |
| C、原命题与逆命题均为真命题 |
| D、原命题与逆命题均为假命题 |
i为虚数单位,则
=( )
| i+1 |
| i-1 |
| A、1 | B、-i | C、i | D、-1 |