题目内容
某次考试结束后,从考号为1-1000号的1000份试卷中,采用系统抽样法抽取50份试卷进行试评,则在考号区间[850,949]之中被抽到的试卷份数为( )
| A、一定是5份 |
| B、可能是4份 |
| C、可能会有10份 |
| D、不能具体确定 |
考点:系统抽样方法
专题:概率与统计
分析:根据系统抽样的定义进行求解即可.
解答:
解:样本间隔为1000÷50=20,
考号区间[850,949]的个数为949-850+1=100,
则100÷20=5,
即一定是5份.
故选:A.
考号区间[850,949]的个数为949-850+1=100,
则100÷20=5,
即一定是5份.
故选:A.
点评:本题主要考查系统抽样的应用,根据条件求出样本间隔是解决本题的关键.

练习册系列答案
相关题目
已知函数g(x)=
,则此函数的最小正周期为( )
| ||
|
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
设函数f(x)=sin22x,则f′(x)等于( )
| A、-2cos4x |
| B、-2sin4x |
| C、2cos4x |
| D、2sin4x |
在某市2014年6月的高二质量检测考试中,理科学生的数学成绩服从正态分布N(98,100).已知参加本次考试的全市理科学生约9 450人.某学生在这次考试中的数学成绩是108分,那么他的数学成绩大约排在全市第( )名?
(参考数值:P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974)
(参考数值:P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974)
| A、1 500 |
| B、1 700 |
| C、4 500 |
| D、8 000 |
设Sn是等差数列{an}的前n项和,S9=18,an-4=30(n>9),已知Sn=336,则n的值为( )
| A、18 | B、19 | C、20 | D、21 |
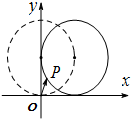 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,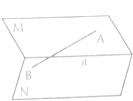 二面角M-a-N中,点A∈M,点B∈N,AB=4
二面角M-a-N中,点A∈M,点B∈N,AB=4