题目内容
求y=x
的导数.
| ax-x2 |
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则和复合函数的导数公式,直接进行求导即可得到结论
解答:
解:∵y=x
=x•(ax-x2)
,
∴y′=(ax-x2)
+x•
(ax-x2)-
•(ax-x2)′=(ax-x2)
+
(ax-x2)-
(a-2x)
| ax-x2 |
| 1 |
| 2 |
∴y′=(ax-x2)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数的导数计算,利用导数的运算法则和复合函数的导数公式是解决本题的关键.

练习册系列答案
相关题目
已知直线l1:x+my+6=0与直线l2:(m-2)x+3y+2m=0垂直,则实数m的值为( )
| A、-1 | ||
B、
| ||
| C、3 | ||
| D、2 |
设函数f(x)=sin22x,则f′(x)等于( )
| A、-2cos4x |
| B、-2sin4x |
| C、2cos4x |
| D、2sin4x |
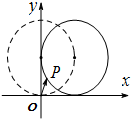 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,