题目内容
已知α∈(
,π),sinα=
.
(1)求cos2α的值;
(2)求cos(
-2α)的值.
| π |
| 2 |
| ||
| 5 |
(1)求cos2α的值;
(2)求cos(
| 5π |
| 6 |
考点:两角和与差的余弦函数,二倍角的余弦
专题:三角函数的求值
分析:(1)利用余弦的倍角公式直接求得;
(2)求出cosα,再由两角差的余弦公式求值.
(2)求出cosα,再由两角差的余弦公式求值.
解答:
解:(1)cos 2α=1-2sin2α …(3分)
=1-2=
,…(5分)
(2)方法一:因为α∈(
,π),sin α=
,∴cos α<0
所以cos α=-
=-
.…(7分)
Sin 2α=2sin α cos α=2×
=-
,…(9分)
所以cos(
-2α)=cos
cos 2α+sin
sin 2α=
+
=-
.…(12分)
方法二:由α∈(
,π),2α∈(π,2π),
∴sin2α<0sin2α=-
=-
=-
…(9分)
所以cos(
-2α)=cos
cos 2α+sin
sin 2α=
+
=-
.…(12分)
=1-2=
| 3 |
| 5 |
(2)方法一:因为α∈(
| π |
| 2 |
| ||
| 5 |
所以cos α=-
| 1-sin2α |
2
| ||
| 5 |
Sin 2α=2sin α cos α=2×
| ||
| 5 |
| 4 |
| 5 |
所以cos(
| 5π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 3 |
| 5 |
| 1 |
| 2 |
4+3
| ||
| 10 |
方法二:由α∈(
| π |
| 2 |
∴sin2α<0sin2α=-
| 1-cos22α |
1-(
|
| 4 |
| 5 |
所以cos(
| 5π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 3 |
| 5 |
| 1 |
| 2 |
4+3
| ||
| 10 |
点评:本题考查了三角函数的化简求值;关键是熟练运用三角函数的倍角公式以及

练习册系列答案
相关题目
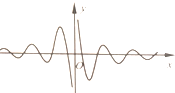 函数y=f(x)的图象如图所示,则f(x)可能是( )
函数y=f(x)的图象如图所示,则f(x)可能是( )| A、xsinx | ||
| B、xcosx | ||
C、
| ||
D、
|
已知直线l1:x+my+6=0与直线l2:(m-2)x+3y+2m=0垂直,则实数m的值为( )
| A、-1 | ||
B、
| ||
| C、3 | ||
| D、2 |
已知函数g(x)=
,则此函数的最小正周期为( )
| ||
|
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
从1,2,3,4,5,…100中任意取3个数,使这3个数恰好成等差数列的不同取法有( )
| A、2440种 |
| B、2450种 |
| C、2500种 |
| D、8550种 |
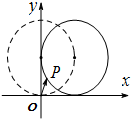 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,