题目内容
17.已知点M(2$\sqrt{2}$,$\frac{2\sqrt{3}}{3}$)在椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且点M到两焦点距离之和为4$\sqrt{3}$.(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A,B两点,以AB为底作等腰三角形,顶点为P(-3,2),求△PAB的面积.
分析 (1)由2a=4$\sqrt{3}$,可得a=2$\sqrt{3}$.又点M(2$\sqrt{2}$,$\frac{2\sqrt{3}}{3}$)在椭圆G上,可得$\frac{2}{3}+\frac{4}{3{b}^{2}}$=1,解得b2,即可得出.
(2)设直线l的方程为y=x+m,与椭圆方程联立得4x2+6mx+3m2-12=0.设A(x1,y1),B(x2,y2)(x1<x2),AB的中点为E(x0,y0),利用中档坐标公式可得E坐标.因为AB是等腰△PAB的底边,所以PE⊥AB.解得m.利用两点之间的距离公式可得|AB|.点P(-3,2)到直线AB:x-y+2=0的距离d,可得△PAB的面积S=$\frac{1}{2}$|AB|•d.
解答 解:(1)∵2a=4$\sqrt{3}$,∴a=2$\sqrt{3}$.
又点M(2$\sqrt{2}$,$\frac{2\sqrt{3}}{3}$)在椭圆G上,∴$\frac{2}{3}+\frac{4}{3{b}^{2}}$=1,解得b2=4,…(4分)
∴椭圆G的方程为:$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}$=1.…(5分)
(2)设直线l的方程为y=x+m,由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得4x2+6mx+3m2-12=0.①
设A(x1,y1),B(x2,y2)(x1<x2),AB的中点为E(x0,y0),
则x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{3m}{4}$,y0=x0+m=$\frac{m}{4}$.
因为AB是等腰△PAB的底边,所以PE⊥AB.
所以PE的斜率k=$\frac{2-\frac{m}{4}}{-3+\frac{3m}{4}}$=-1,解得m=2.…(10分)
此时方程①为4x2+12x=0,解得x1=-3,x2=0,
所以y1=-1,y2=2.
所以|AB|=3$\sqrt{2}$.
此时,点P(-3,2)到直线AB:x-y+2=0的距离d=$\frac{|-3-2+2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
所以△PAB的面积S=$\frac{1}{2}$|AB|•d=$\frac{9}{2}$.…(12分)
点评 本题考查了椭圆的标准方程及其性质、等腰三角形的性质、相互垂直的直线斜率之间的关系、点到直线的距离公式、两点之间的距离公式、三角形面积计算公式,考查了推理能力与计算能力,属于难题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | $2\overrightarrow{DB}+3\overrightarrow{DC}=0$ | B. | $3\overrightarrow{DB}+2\overrightarrow{DC}=0$ | C. | $\overrightarrow{OA}-5\overrightarrow{OD}=0$ | D. | $5\overrightarrow{OA}+\overrightarrow{OD}=0$ |
| A. | 1 | B. | -1 | C. | i | D. | -i |
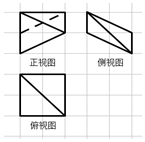 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |