题目内容
3.设a>0且a≠1,函数f(x)=loga$\frac{x-3}{x+3}$,g(x)=1+loga(x-1),两函数的定义域分别为集合A、B,若将A∩B记作区间D.(1)试求函数f(x)在D上的单调性;
(2)若[m,n]⊆D,函数f(x)在[m,n]上的值域恰好为[g(n),g(m)],求a的取值范围.
分析 (1)变形得出f(x)=loga(1$-\frac{6}{x+3}$),据复合函数单调性可以判断.
(2)函数f(x)在[m,n]上的值域恰好为[g(n),g(m)],
g(x)单调递减函数.得出0<a<1,再利用函数性质得出1$-\frac{6}{x+3}$=a(x-1)有2个根,分离参数利用基本不等式求解即可.
解答 解:(1)∵设a>0且a≠1,函数f(x)=loga$\frac{x-3}{x+3}$,
g(x)=1+loga(x-1),
∴$\frac{x-3}{x+3}$>0即x>3或x<-3
x-1>0,x>1
∴A={x|x>3或x<-3}
B+{x|x>1}
∴D=(3,+∞)
∵函数f(x)=loga$\frac{x-3}{x+3}$,
∴f(x)=loga(1$-\frac{6}{x+3}$),
∵u(x)=1$-\frac{6}{x+3}$在(3,+∞)上单调递增
∴据复合函数单调性得出:
当a>1时,f(x)=loga(1$-\frac{6}{x+3}$)为增函数;
当0<a<1时,f(x)=loga(1$-\frac{6}{x+3}$)为减函数;
(2)∵函数f(x)在[m,n]上的值域恰好为[g(n),g(m)],
∴g(x)单调递减函数,
∴0<a<1,
∴当0<a<1时,f(x)=loga(1$-\frac{6}{x+3}$)为减函数
∴1$-\frac{6}{x+3}$=a(x-1)有2个根,
即$\frac{1}{a}$=(x-3)$+\frac{12}{x-3}$+8,x>3
根据不等式得出:(x-3)$+\frac{12}{x-3}$+8≥4$\sqrt{3}$+8
$\frac{1}{a}$≥4$\sqrt{3}$+8,
∴0<a≤$\frac{1}{4\sqrt{3}+8}$
点评 本题考察了函数的性质,不等式,构造思想,转化思想,属于中档题.

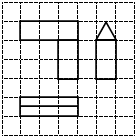 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 2+$\frac{\sqrt{3}}{4}$ | D. | 3+$\frac{\sqrt{3}}{3}$ |
| A. | -7 | B. | $-\frac{1}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,-1)∪(-1,+∞) | C. | (-∞,1),(1,+∞) | D. | (-∞,-1),(-1,+∞) |
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| 数学优秀 | 数学不优秀 | 总计 | |
| 化学优秀 | 60 | 100 | 160 |
| 化学不优秀 | 140 | 500 | 640 |
| 总计 | 200 | 600 | 800 |
| p(K2>k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |