题目内容
14.已知圆C:x2+y2+8x+12=0,若直线y=kx-2与圆C至少有一个公共点,则实数k的取值范围为$[{-\frac{4}{3},0}]$.分析 由题意利用点到直线的距离小于半径,求出k的范围即可.
解答 解:由题意可知圆的圆心坐标为(-4,0),半径为2,
因为圆C:x2+y2+8x+12=0,若直线y=kx-2与圆C至少有一个公共点,所以$\frac{|-4k-2|}{\sqrt{{k}^{2}+1}}$≤2,
解得k∈$[{-\frac{4}{3},0}]$.
故答案为$[{-\frac{4}{3},0}]$.
点评 本题是中档题,考查直线与圆的位置关系,考查计算能力,转化思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.$\sqrt{1-{{sin}^2}\frac{π}{5}}$的化简结果是( )
| A. | $cos\frac{π}{5}$ | B. | $-cos\frac{π}{5}$ | C. | $±cos\frac{π}{5}$ | D. | $sin\frac{π}{5}$ |
19.下列有关命题的说法错误的为( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “|x|<2”是“x2-x-6<0”的充分不必要条件 | |
| C. | 命题“存在∈R,使得x2+x+1<0”的否定是“对任意x∈R,均有x2+x+1≥0” | |
| D. | 若p∧q为假命题,则p,q均为假 |
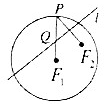 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.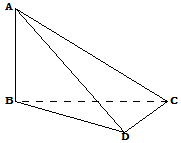 在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1,AB=2
在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1,AB=2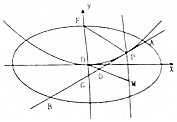 平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.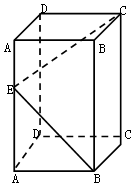 长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )
长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )