题目内容
19.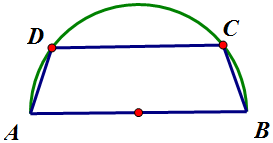 有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.
有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.(1)若这个梯形上底为CD=2a,求它的腰长x;
(2)求出这个梯形的周长y关于腰长x的函数解析式,并指出它的定义域;
(3)求这个梯形周长的最大值,并求出当它最大时,梯形的面积S.
分析 (1)由题意利用等腰梯形、圆、勾股定理列出方程,能求出它的腰长.
(2)由腰长得$2a=\frac{{4-{x^2}}}{2}$,由此能求出求出这个梯形的周长y关于腰长x的函数解析式,并指出它的定义域.
(3)由二次函数性质能求出结果.
解答 解:(1)∵22-a2=x2-(2-a)2
∴x2=8-4a,
∴它的腰长$x=\sqrt{8-4a}$…(4分)
(2)由(1)知:$2a=\frac{{4-{x^2}}}{2}$,
∴$y=2x+\frac{{4-{x^2}}}{2}+4=-\frac{1}{2}{x^2}+x+6$,
∵$a>0∴x<2\sqrt{2}$,∴定义域为$(0,2\sqrt{2})$…(8分)
(3)由(2)知,x=1时,y最大
此时梯形的上底$2a=\frac{7}{2}$,高$h=\frac{{\sqrt{15}}}{4}$,
∴$S=\frac{1}{2}(\frac{7}{2}+4)•\frac{{\sqrt{15}}}{4}=\frac{{15\sqrt{15}}}{16}$.
点评 本题考查函数在生产生活中的实际应用,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
11.若直线l的一个方向向量$\overrightarrow a=(2,2,-2)$,平面α的一个法向量为$\overrightarrow b=(1,1,-1)$,则( )
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
8.已知奇函数f(x)满足f(x+2)=f(x),当x∈(0,1)时,函数f(x)=2x,则$f({log_{\frac{1}{2}}}23)$=( )
| A. | $-\frac{16}{23}$ | B. | $-\frac{23}{16}$ | C. | $\frac{16}{23}$ | D. | $\frac{23}{16}$ |
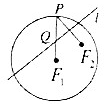 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.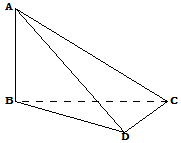 在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1,AB=2
在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1,AB=2