题目内容
15.以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}{x=tsinφ}\\{y=1+tcosφ}\end{array}\right.$(t为参数,0<φ<π,曲线C的极坐标方程为ρcos2θ=4sinθ.(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当φ变化时,求|AB|的最小值.
分析 (1)把直线参数方程中的参数t消去,即可得到直线l的普通方程,把x=ρcosθ,y=ρsinθ代入曲线C的极坐标方程化直角坐标方程;
(2)将直线的参数方程代入曲线C的直角坐标方程,利用根与系数的关系结合t的几何意义求得|AB|的最小值.
解答 解:(1)由$\left\{\begin{array}{l}{x=tsinφ}\\{y=1+tcosφ}\end{array}\right.$,消去t得l的普通方程xcosφ-ysinφ+sinφ=0,
由ρsin2θ=4cosθ,得(ρsinθ)2=4ρcosθ,
把x=ρcosθ,y=ρsinθ代入上式,得y2=4x,
∴曲线C的直角坐标方程为x2=4y;
(2)将直线l的参数方程代入y2=4x,得t2sin2φ-4tcosφ-4=0,
设A、B两点对应的参数分别为t1,t2,
则${t}_{1}+{t}_{2}=\frac{4cosφ}{si{n}^{2}φ}$,${t}_{1}{t}_{2}=\frac{-4}{si{n}^{2}φ}$.
∴|AB|=$|{t}_{1}-{t}_{2}|=\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\frac{4}{si{n}^{2}φ}$.
当φ=$\frac{π}{2}$时,即sin2φ=1,|AB|的最小值为4.
点评 本题考查参数方程化普通方程,考查直线参数方程中参数几何意义的应用,是基础题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
10.已知向量$\overrightarrow{a}$=(x,$\sqrt{3}$),$\overrightarrow{b}$=(x,-$\sqrt{3}$),若(2$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
6.若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多一个公共点,则实数k的取值范围是( )
| A. | (-∞,3] | B. | [9,+∞) | C. | (-∞,9] | D. | (-∞,9) |
3.下列结论不正确的是( )
| A. | 若y=3,则y'=0 | B. | 若$y=\frac{1}{{\sqrt{x}}}$,则$y'=-\frac{{\sqrt{x}}}{2}$ | C. | 若$y=\sqrt{x}$,则$y'=\frac{1}{{2\sqrt{x}}}$ | D. | 若y=x,则y'=1 |
20.已知tanα=-$\frac{3}{4}$,tan(π-β)=$\frac{1}{2}$,则tan(α-β)的值为( )
| A. | -$\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | -$\frac{11}{2}$ |
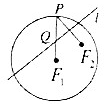 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.