题目内容
在△ABC中，a、b、c是角A、B、C的对边，已知b=2
，A，B，C成等差数列，则△ABC的外接圆的半径等于 ．
| 3 |
考点：正弦定理,等差数列的性质
专题：解三角形
分析：根据条件求出B，利用正弦定理即可得到结论．
解答：
解：∵A，B，C成等差数列，
∴A+C=2B，即3B=π，
∴B=
，
由正弦定理
=2R得R=
=
=2，
即△ABC的外接圆的半径等于2，
故答案为：2．
∴A+C=2B，即3B=π，
∴B=
| π |
| 3 |
由正弦定理
| b |
| sinB |
| b |
| 2sinB |
2
| ||||
2×
|
即△ABC的外接圆的半径等于2，
故答案为：2．
点评：本题主要考查正弦定理的应用，利用条件求出B的大小是解决本题的关键，比较基础．
练习册系列答案
相关题目
如果x＞y＞0，则
=（ ）
| xyyx |
| xxyy |
A、(x-y)
| ||
B、(x-y)
| ||
C、(
| ||
D、(
|
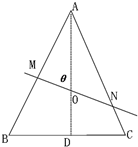如图，等边△ABC中，AB=3，O为中心，过O的直线交AB于M，交AC于N，设∠AOM=θ（0≤θ≤120°），当θ分别为何值时，