题目内容
11.在△ABC中,$a=3,c=2,B=\frac{π}{3}$,则b=( )| A. | 19 | B. | 7 | C. | $\sqrt{19}$ | D. | $\sqrt{7}$ |
分析 根据题意,将a、c、B的值代入余弦定理b2=a2+c2-2accosB中,可得b2的值,进而可得b的值,即可得答案.
解答 解:根据题意,△ABC中,$a=3,c=2,B=\frac{π}{3}$,
则b2=a2+c2-2accosB=9+4-6=7,
即b=$\sqrt{7}$;
故选:D.
点评 本题考查余弦定理的应用,熟练运用余弦定理是解题的关键.

练习册系列答案
相关题目
1.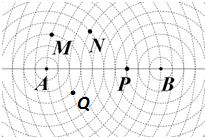 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )| A. | eM<eN<eQ<eP | B. | eN<eM<eP<eQ | C. | eP<eQ<eM<eN | D. | eQ<eN<eM<eP |
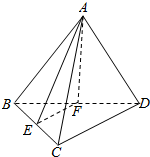 如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.
如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.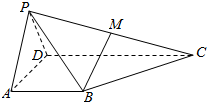 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD,AB⊥AD,AB∥CD,点M是PC的中点.