题目内容
16.已知函数$f(x)=2\sqrt{3}sinxcosx+2{cos^2}x-1({x∈R})$.(1)求函数f(x)的最小正周期及单调递增区间;
(2)当$x∈[{0,\frac{π}{2}}]$时,m-2≤f(x)≤m+2恒成立,求实数m的取值范围.
分析 (1)利用二倍角公式与和角公式对f(x)进行化简,结合正弦函数的单调性列出不等式解出单调区间;
(2)求出f(x)在[0,$\frac{π}{2}$]上的值域U,令U⊆[m-2,m+2]列出不等式组解出m的范围..
解答 解:(1)f(x)=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$).∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
令-$\frac{π}{2}$+2kπ≤2x$+\frac{π}{6}$≤$\frac{π}{2}$+2kπ,解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}+kπ$.∴f(x)的单调递增区间是[-$\frac{π}{3}$+kπ,$\frac{π}{6}+kπ$.],k∈Z.
(2)∵$x∈[{0,\frac{π}{2}}]$,∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],∴当2x+$\frac{π}{6}$=$\frac{π}{2}$时,f(x)取得最大值2,当2x+$\frac{π}{6}$=$\frac{7π}{6}$时,f(x)取得最小值-1.
∵m-2≤f(x)≤m+2恒成立,∴$\left\{\begin{array}{l}{m-2≤-1}\\{2≤m+2}\end{array}\right.$,解得0≤m≤1.
∴实数m的取值范围是[0,1].
点评 本题考查了三角函数的恒等变换,三角函数的单调性,三角函数的值域,属于中档题.

练习册系列答案
相关题目
11.下列各式中,值为$\frac{1}{2}$的是( )
| A. | sin15°cos15° | B. | cos2$\frac{π}{12}$-sin2$\frac{π}{12}$ | ||
| C. | $\frac{tan22.5°}{1-ta{n}^{2}22.5°}$ | D. | $\frac{1+tan15°}{1-tan15°}$ |
1.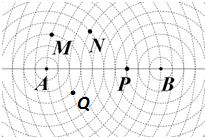 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )| A. | eM<eN<eQ<eP | B. | eN<eM<eP<eQ | C. | eP<eQ<eM<eN | D. | eQ<eN<eM<eP |
5.动点P(x,y)满足$\left\{\begin{array}{l}{y≥1}\\{x+2y≤5}\\{x+y≥3}\end{array}\right.$,点Q为(1,-1),O为原点,λ|$\overrightarrow{OQ}$|=$\overrightarrow{OP}•\overrightarrow{OQ}$,则λ的最大值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
6.过点A(m,1),B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线垂直,则m的值为( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |