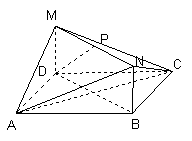
题目内容
在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,
(Ⅰ)求证:DP∥平面ANC;
(Ⅱ)求二面角N-AC-B的余弦值.
(Ⅰ)证明:连接BD交AC于O,连接NO,……………………………1分
 ∵四边形ABCD,BDMN都是矩形,
∵四边形ABCD,BDMN都是矩形,
∴O是BD的中点,又P是MN的中点,
∴PN∥DO
∴四边形PNOD是平行四边形,
∴DP∥ON………………………………2分
又DP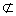 平面ANC,NO
平面ANC,NO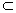 平面ANC
平面ANC
∴DP∥平面ANC;……………………………4分
(Ⅱ)解法一:作BH垂直于AC于H连接NH ,……………………………………………………6分
∵MD⊥平面ABCD,DM∥NB,
∴NH⊥平面ABCD,
由三垂线定理得:NH⊥AC,…………………………………8分
∴∠NHB是二面角N-AC-B的平面角,………………………9分
在RT△NBH中,
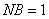 ,
,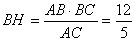 ,
, ,…………………11分
,…………………11分
∴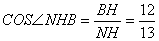 ,
,
∴二面角N-AC-B的余弦值为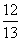 …………………………12分
…………………………12分
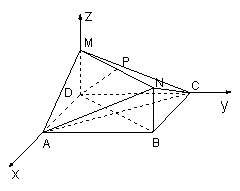 解法二:建立如图所示的坐标系,
解法二:建立如图所示的坐标系,
则:A(3,0,0),C(0,4,0),N(3,4,1),………………………………………………7分
设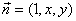 是平面ANC的一个法向量,
是平面ANC的一个法向量,
又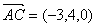 ,
,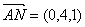
则
解得: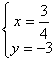
∴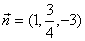 ………………………9分
………………………9分
又 是平面ABC的一个法向量,……………………………10分
是平面ABC的一个法向量,……………………………10分
设二面角N-AC-B的大小为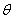 ,
,
则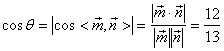 ,
,
∴二面角N-AC-B的余弦值为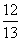 ……………………………………………12分
……………………………………………12分

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 , 若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则
, 若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则 的最小值为( )
的最小值为( ) C.
C.  D. 7
D. 7 是直线,
是直线, 是两个不同的平面
是两个不同的平面  B.若
B.若
 ,则
,则
 ,则
,则 D.若
D.若
 ⊥
⊥ 表示的平面区域的面积为4,点
表示的平面区域的面积为4,点 在所给平面区域内,则
在所给平面区域内,则 的最大值为 .
的最大值为 .  ,集合
,集合 ,
,  ,则图中的阴影部分表示的集合为
,则图中的阴影部分表示的集合为 B.
B. C.
C. D.
D. 

 体积是 ( )
体积是 ( ) ”是“直线
”是“直线 与直线
与直线 互相垂直”的
互相垂直”的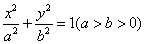 的左、右焦点分别为
的左、右焦点分别为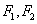 ,离心率为
,离心率为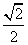 ,P是椭圆上一点,且
,P是椭圆上一点,且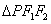 面积的最大值等于2.
面积的最大值等于2.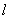 与直线
与直线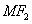 垂直,试判断直线
垂直,试判断直线