题目内容
7.我们知道:在平面内,点(x0,y0)到直线Ax+By+C=0的距离公式为d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$,通过类比的方法,可求得:在空间中,点(2,4,1)到平面x+2y+3z+3=0的距离为( )| A. | 3 | B. | 5 | C. | $\frac{8\sqrt{14}}{7}$ | D. | 3$\sqrt{5}$ |
分析 类比点P(x0,y0)到直线Ax+By+C=0的距离d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$,可知在空间中,d=$\frac{|2+8+3+3|}{\sqrt{1+4+9}}$=$\frac{8\sqrt{14}}{7}$.
解答 解:类比点P(x0,y0)到直线Ax+By+C=0的距离d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$,
可知在空间中,
点(2,4,1)到平面x+2y+3z+3=0的距离d=$\frac{|2+8+3+3|}{\sqrt{1+4+9}}$=$\frac{8\sqrt{14}}{7}$.
故选C.
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.将边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D.则四面体ABCD的内切球的半径为( )
| A. | 1 | B. | $2\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{3}$ |
12.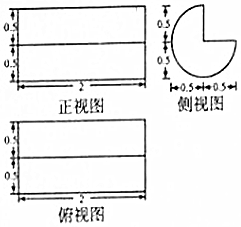 某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
 某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )| A. | 94.20元 | B. | 240.00元 | C. | 282.60元 | D. | 376.80元 |
19.等比数列{an}的前n项和为Sn,已知S1,2S2,3S3成等差数列,则{an}的公比为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
16.先把函数y=sin(x+φ)的图象上个点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再向右平移$\frac{π}{3}$个单位,所得函数关于y轴对称,则φ的值可以是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |