题目内容
已知双曲线的焦点在x轴上,两个顶点间的距离为2,焦点到渐近线的距离为 .
.
(1)求双曲线的标准方程;
(2)写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程.
 .
.(1)求双曲线的标准方程;
(2)写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程.
(1)x2-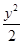 =1(2)y=±
=1(2)y=± x.
x.
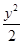 =1(2)y=±
=1(2)y=± x.
x.(1)依题意可设双曲线的方程为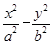 =1(a>0,b>0),则2a=2,所以a=1.设双曲线的一个焦点为(c,0),一条渐近线的方程为bx-ay=0,则焦点到渐近线的距离d=
=1(a>0,b>0),则2a=2,所以a=1.设双曲线的一个焦点为(c,0),一条渐近线的方程为bx-ay=0,则焦点到渐近线的距离d=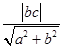 =b=
=b= ,所以双曲线的方程为x2-
,所以双曲线的方程为x2-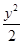 =1.
=1.
(2)双曲线的实轴长为2,虚轴长为2 ,焦点坐标为(-
,焦点坐标为(-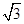 ,0),(
,0),(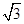 ,0),离心率为
,0),离心率为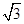 ,渐近线方程为y=±
,渐近线方程为y=± x.
x.
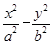 =1(a>0,b>0),则2a=2,所以a=1.设双曲线的一个焦点为(c,0),一条渐近线的方程为bx-ay=0,则焦点到渐近线的距离d=
=1(a>0,b>0),则2a=2,所以a=1.设双曲线的一个焦点为(c,0),一条渐近线的方程为bx-ay=0,则焦点到渐近线的距离d=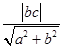 =b=
=b= ,所以双曲线的方程为x2-
,所以双曲线的方程为x2-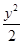 =1.
=1.(2)双曲线的实轴长为2,虚轴长为2
 ,焦点坐标为(-
,焦点坐标为(-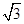 ,0),(
,0),(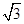 ,0),离心率为
,0),离心率为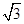 ,渐近线方程为y=±
,渐近线方程为y=± x.
x.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
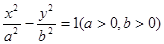 的左、右焦点分别为
的左、右焦点分别为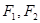 ,若
,若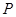 为其上一点,且
为其上一点,且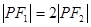 ,
,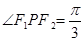 ,则双曲线的离心率为( )
,则双曲线的离心率为( )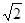
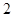
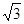
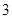
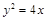 的准线过双曲线
的准线过双曲线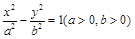 的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为
的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为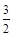 ,则双曲线的离心率为( )
,则双曲线的离心率为( )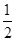 的两条双曲线成为“相近双曲线”。已知双曲线
的两条双曲线成为“相近双曲线”。已知双曲线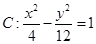 ,则下列双曲线中与
,则下列双曲线中与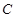 是“相近双曲线”的为( )
是“相近双曲线”的为( )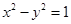

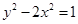
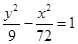
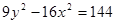 的离心率为 .
的离心率为 .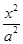 -
-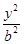 =1(a>0,b>0)的渐近线没有公共点,则此双曲线的离心率可以是( )
=1(a>0,b>0)的渐近线没有公共点,则此双曲线的离心率可以是( )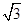
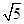
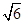
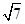
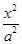 -
-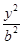 =1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .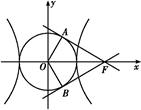
 -y2=1的一个焦点为(2,0),则它的离心率为________.
-y2=1的一个焦点为(2,0),则它的离心率为________.