题目内容
根据已知条件求范围：
（1）求满足sinα＞
的角α的取值范围；
（2）求满足sinα＞cosα的角的α的取值范围．
（1）求满足sinα＞
| ||
| 2 |
（2）求满足sinα＞cosα的角的α的取值范围．
考点：任意角的三角函数的定义
专题：三角函数的图像与性质
分析：（1）根据三角函数的图象和性质，解不等式即可得到结论．
（2）转化sinα＞cosα为正切函数，利用正弦函数的图象与性质，求解角的α的取值范围．
（2）转化sinα＞cosα为正切函数，利用正弦函数的图象与性质，求解角的α的取值范围．
解答：
解：（1）因为sinα＞
，所以2kπ+
＜α＜2kπ+
，k∈Z，
角α的取值范围(2kπ+
，2kπ+
)k∈Z；
（2）sinα＞cosα化为：taα＞1，由正切函数的图象与性质可得，α＞kπ+
，k∈Z，
∴角的α的取值范围：（kπ+
，+∞）k∈Z．
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
角α的取值范围(2kπ+
| π |
| 3 |
| 2π |
| 3 |
（2）sinα＞cosα化为：taα＞1，由正切函数的图象与性质可得，α＞kπ+
| π |
| 4 |
∴角的α的取值范围：（kπ+
| π |
| 4 |
点评：本题考查正弦函数、正切函数的图象与性质，考查三角函数图象的应用能力，属于中档题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
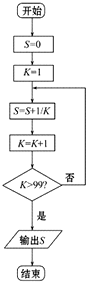给出一个算法的程序框图（如图所示）．
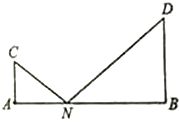如图，C，D是两个小区的所在地，C，D到一条公路AB的垂直距离CA=1km，DB=2km，AB两端之间的距离为4km，某公交公司将在AB之间找一点N，在N处建造一个公交站台．
如图所示，等边△ABC的边长为2，以A为圆心，半径为1作圆，PQ是圆的直径，求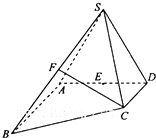
如图，在四棱锥S-ABCD中，己如AB∥DC，AB⊥AD，△SAD是正三角形，AD=AB=2DC=2，SC=