题目内容
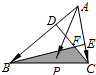如图，D、E是△ABC边AB、AC上的点，已知AB=3AD，AE=2EC，BE交CD于点F，点P是△FBC内（含边界）一点，若| AP |
| AB |
| AE |
A、[
| ||
B、[
| ||
C、[1，
| ||
| D、[1，2] |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：因点P是阴影内任一点，所以可在阴影内任取点P，因为条件中是用
，
表示的
，所以也想着用
，
来表示
．根据向量的加法运算，连接BP并延长交AC于G点，这时
=
+
，并设
=m，
=n，并求出m，n的取值范围，这样便完成了用
，
表示
了．从而用m，n表示λ+μ，根据m，n的范围就可求出λ+μ的范围．求到这之后，好要求几个点处的λ+μ的取值，综合起来就得到了λ+μ的范围了．
| AB |
| AE |
| AP |
| AB |
| AE |
| AP |
| AP |
| AE |
| EP |
| EG |
| AE |
| GP |
| GB |
| AB |
| AE |
| AP |
解答：
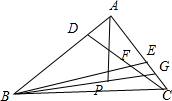解：如下图，在阴影区域任找一点P，连接BP，并延长交AC于G，设
=m，
=n则：
0＜m＜
，0＜n＜1，AG=（m+1）AE，∴
=
+
=(m+1)
+n
=(m+1)
+n(
-
)
=n
+(m+1-mn-n)
，∴λ+μ=m（1-n）+1
∵0＜m＜
，0＜1-n＜1，∴0＜m(1+n)＜
，∴0＜λ+μ＜
，下面求P与B，E，C重合的情况．
P在B点时：
=1•
+0•
，∴λ+μ=1；
P在B点时：
=0•
+
，∴λ+μ=
；
P在F点时：过E作EH∥AB，由条件知，
=
，∴
=
，∴EF=
．
∴
=
+
=
+
，∴λ+μ=1，综上得λ+μ的取值范围是：[1，
]．
故选：C．
解：如下图，在阴影区域任找一点P，连接BP，并延长交AC于G，设| EG |
| AE |
| GP |
| GB |
0＜m＜
| 1 |
| 2 |
| AP |
| AG |
| GP |
| AE |
| GB |
| AE |
| AB |
| AG |
=n
| AB |
| AE |
∵0＜m＜
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
P在B点时：
| AP |
| AB |
| AE |
P在B点时：
| AP |
| AB |
| 3 |
| 2 |
| AE |
| 3 |
| 2 |
P在F点时：过E作EH∥AB，由条件知，
| EH |
| AD |
| 1 |
| 3 |
| EH |
| BD |
| 1 |
| 6 |
| 1 |
| 7 |
| EB |
∴
| AP |
| AE |
| 1 |
| 7 |
| EB |
| 1 |
| 7 |
| AB |
| 6 |
| 7 |
| AE |
| 3 |
| 2 |
故选：C．
点评：求解本题的关键便是设
=m，
=n，而不能忽略的是求几个点处的取值．注意运用向量的运算．
| EG |
| AE |
| GP |
| GB |
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的一条渐近线与曲线y=
相切，且右焦点F为抛物线y2=20x的焦点，则双曲线的标准方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x-1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
已知双曲线C：
-
=1（b＞0）的一条渐进线方程为y=
x，F1，F2分别为双曲线C的左右焦点，P为双曲线C上的一点，满足|PF1|：|PF2|=3：1，则|
+
|的值是（ ）
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
| A、4 | ||||
B、2
| ||||
C、2
| ||||
D、
|
当输入x=-4时，如图的程序运行的结果是（ ）
| A、7 | B、8 | C、9 | D、15 |
某款手机的广告宣传费用x（单位万元）与利润y（单位万元）的统计数据如下表：
根据上表可得线性回归方程
=
x+
中的
为9.4，据此模型预报广告宣传费用为10万元时利润为（ ）
| 广告宣传费用x | 6 | 5 | 7 | 8 |
| 利润y | 34 | 26 | 38 | 42 |
 |
| y |
|
| b |
|
| a |
| ? |
| b |
| A、65.0万元 |
| B、67.9万元 |
| C、68.1万元 |
| D、68.9万元 |
已知点P（x，y）是双曲线C：x2-y2=a（a＞0）右支上动点，双曲线C的过点P的切线分别交两条渐近线于点A，B，则△OAB的面积是（ ）
| A、随x的增大而增大 |
| B、随x的增大而减小 |
| C、a2 |
| D、a |