题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线与曲线y=
相切,且右焦点F为抛物线y2=20x的焦点,则双曲线的标准方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x-1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线的右焦点F为抛物线y2=20x的焦点,可得a2+b2=25①,利用双曲线
-
=1(a>0,b>0)的一条渐近线与曲线y=
相切,可得1-
=0②,由①②可得a2=20,b2=5,即可求出双曲线的标准方程.
| x2 |
| a2 |
| y2 |
| b2 |
| x-1 |
| 4b2 |
| a2 |
解答:
解:∵双曲线的右焦点F为抛物线y2=20x的焦点,
∴F(5,0),即a2+b2=25①.
y=
x代入y=
,可得
x2-x+1=0,
∵双曲线
-
=1(a>0,b>0)的一条渐近线与曲线y=
相切,
∴△=1-
=0②,
由①②可得a2=20,b2=5,
∴双曲线的标准方程为
-
=1.
故选:A.
∴F(5,0),即a2+b2=25①.
y=
| b |
| a |
| x-1 |
| b2 |
| a2 |
∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| x-1 |
∴△=1-
| 4b2 |
| a2 |
由①②可得a2=20,b2=5,
∴双曲线的标准方程为
| x2 |
| 20 |
| y2 |
| 5 |
故选:A.
点评:本题考查双曲线的标准方程,考查抛物线的性质,考查学生的计算能力,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图正方体ABCD-A1B1C1D1,把一根拉紧的细绳两端分别系在AC1两点,此时这个正方体的正视图可能是( )


| A、①② | B、②③ | C、②④ | D、③④ |
函数f(x)=
的最大值为M,最小值为N,则( )
| ||||
| 2x2+cosx |
| A、M-N=4 |
| B、M+N=4 |
| C、M-N=2 |
| D、M+N=2 |
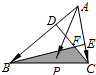 如图,D、E是△ABC边AB、AC上的点,已知AB=3AD,AE=2EC,BE交CD于点F,点P是△FBC内(含边界)一点,若
如图,D、E是△ABC边AB、AC上的点,已知AB=3AD,AE=2EC,BE交CD于点F,点P是△FBC内(含边界)一点,若| AP |
| AB |
| AE |
A、[
| ||
B、[
| ||
C、[1,
| ||
| D、[1,2] |