题目内容
求函数f(x)=
(x≥0)的最大值.
| ||
x+
|
考点:函数的最值及其几何意义
专题:函数的性质及应用,导数的概念及应用
分析:先求导,令导数为0,利用导数求极值然后求最值.
解答:
解:∵函数f(x)=
,
∴f′(x)=
,
=
,
=
=
,
∵x≥0,
∴(x+
)2
>0,
∴令f′(x)=0得x=1,
且0<x<1时,f′(x)>0,函数单调递增;当x>1时,f′(x)<0;
∴x=1时取得最大值f(1)=
.
| ||
x+
|
∴f′(x)=
(
| ||||||||
(x+
|
=
| ||||||||||
(x+
|
=
(x+1)(x+
| ||||
(x+
|
=
-
| ||||
(x+
|
∵x≥0,
∴(x+
| 1 |
| 2 |
| x2+2x |
∴令f′(x)=0得x=1,
且0<x<1时,f′(x)>0,函数单调递增;当x>1时,f′(x)<0;
∴x=1时取得最大值f(1)=
2
| ||
| 3 |
点评:本题考查函数的单调性和求最值,利用导数求极值然后求最值,是常用方法.

练习册系列答案
相关题目
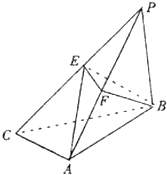 如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4
如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4