题目内容
已知过定点(2,0)的直线与抛物线x2=y相交于A(x1,y1),B(x2,y2)两点.若x1,x2是方程x2+xsinα-cosα=0的两个不相等实数根,则tanα的值是( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
考点:根与系数的关系,函数的零点与方程根的关系
专题:函数的性质及应用
分析:根据x1,x2是方程x2+xsinα-cosα=0的两个不相等的实数根,可得x1+x2 =-sinα,x1•x2 =-cosα.设过定点(2,0)的直线的方程为y=k(x-2),代入抛物线x2=y可得x2-kx+2k=0,故有 x1+x2 =k,x1•x2 =2k,由此求得tanα=
的值.
| sinα |
| cosα |
解答:
解:∵x1,x2是方程x2+xsinα-cosα=0的两个不相等的实数根,
∴x1+x2 =-sinα,x1•x2 =-cosα.
设过定点(2,0)的直线的方程为y=k(x-2),则由题意可得k<0,
把此直线方程代入抛物线x2=y可得 x2-kx+2k=0∴x1+x2 =k,x1•x2 =2k,
∴sinα=-k,cosα=-2k,tanα=
=
,
故选:A.
∴x1+x2 =-sinα,x1•x2 =-cosα.
设过定点(2,0)的直线的方程为y=k(x-2),则由题意可得k<0,
把此直线方程代入抛物线x2=y可得 x2-kx+2k=0∴x1+x2 =k,x1•x2 =2k,
∴sinα=-k,cosα=-2k,tanα=
| sinα |
| cosα |
| 1 |
| 2 |
故选:A.
点评:本题主要考查一元二次方程根与系数的关系,同角三角函数的基本关系,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
执行如图所示的程序框图,则输出S的值为( )
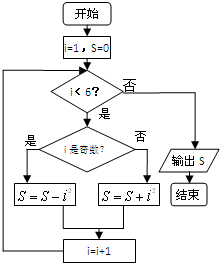

| A、3 | B、-6 | C、10 | D、-15 |
已知椭圆
+
=1(a>0)与双曲线
-
=1有相同的焦点,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| 9 |
| x2 |
| 4 |
| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x,y满足方程(x-2)2+y2=1,那么
的最大值为( )
| y |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
条件p:x≥0,条件q:x2≤x,则p是q的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.