题目内容
对一切实数x,所有的二次函数f(x)=ax2+bx+c(a<b)的值均为非负实数,则
的最大值是( )
| b-a |
| a+b+c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:设b-a=k,由△≤0,可得c≥
.可得
=
≤
=
,再利用基本不等式求得它的最大值.
| (a+k)2 |
| 4a |
| b-a |
| a+b+c |
| k |
| 2a+k+c |
| k | ||
2a+k+
|
| 1 | ||||||
|
解答:
解:设b-a=k,则b=a+k,且△=b2-4ac=(a+k)2-4ac≤0,
∴c≥
.
∴
=
≤
=
=
≤
=
,
故选:A.
∴c≥
| (a+k)2 |
| 4a |
∴
| b-a |
| a+b+c |
| k |
| 2a+k+c |
| k | ||
2a+k+
|
| k | ||||||
|
| 1 | ||||||
|
| 1 | ||||
2×
|
| 1 |
| 3 |
故选:A.
点评:本题主要考查二次函数的性质,基本不等式的应用,注意用放缩法,属于基础题.

练习册系列答案
相关题目
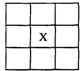 将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )
将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(2,1),
=(-3,4),则
-
的坐标为( )
| a |
| b |
| a |
| b |
| A、(-5,3) |
| B、(-1,5) |
| C、(5,-3) |
| D、(1,-5) |
在平行四边形ABCD中,
+
等于( )
| AB |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、|
|
若直线ax-2y-1=0与直线x+y-2=0互相垂直,则a的值为( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
 如图所示,一个空间几何体的正视图和侧视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和侧视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的体积为( )| A、12π | B、14π |
| C、16π | D、20π |

