题目内容
若直线ax-2y-1=0与直线x+y-2=0互相垂直，则a的值为（ ）
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：由题意可得，这两条直线的斜率之积等于-1，由此求得a的值．
解答：
解：∵直线ax-2y-1=0与直线x+y-2=0互相垂直，∴它们的斜率之积等于-1，
即
×(-1)=-1，求得a=2，
故选：D．
即
| a |
| 2 |
故选：D．
点评：本题主要考查两直线垂直的性质，属于基础题．
练习册系列答案
相关题目
对一切实数x，所有的二次函数f（x）=ax2+bx+c（a＜b）的值均为非负实数，则
的最大值是（ ）
| b-a |
| a+b+c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
已知|
|=6，|
|=3，
•
=-12，则向量
在向量
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、4 | D、-4 |
角α的终边经过点P（3，4），则sinα=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数在（1，+∞）为增函数的是（ ）
| A、y=x2-4x | ||
| B、y=|x-2| | ||
C、y=
| ||
| D、y=log0.5x |
函数f（x）=
定义域是（ ）
| 1 | ||
|
| A、{x|x＞5} |
| B、{x|x＜5} |
| C、{x|x≥5} |
| D、{x|x≠5} |
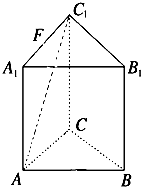正三棱柱ABC-A1B1C1中底面边长为a，侧棱长为