题目内容
某售房部销售人员小刚统计了自己近五年的售房套数,其数据如表:
(I)利用所给数据,求售房套数与年份之间的回归直线方程
=kx+a,并判断它们之间是正相关还是负相关;
(Ⅱ)利用(I)中所求出的回归直线方程预测2014年小刚可能售出的房屋套数.
参考公式:b=
=
,a=
-b
.
| 年份x/年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 售房y/套 | 97 | 98 | 103 | 108 | 109 |
 |
| y |
(Ⅱ)利用(I)中所求出的回归直线方程预测2014年小刚可能售出的房屋套数.
参考公式:b=
| |||||||
|
| |||||||
|
. |
| y |
. |
| x |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)先利用数据平均值的公式求出x,y的平均值,再计算b,a的值,即可求出售房套数与年份之间的回归直线方程,根据b>0,可得售房套数与年份成正相关关系;
(2)x=2014,代入回归直线方程,即可预测该教师2014年小刚可能售出的房屋套数.
(2)x=2014,代入回归直线方程,即可预测该教师2014年小刚可能售出的房屋套数.
解答:
解:(1)由题意,
=
(2009+2010+2011+2012+2013)=2011,
=
(97+98+103+108+109)=103,…(2分)
∴b=
=3.4…(4分)
a=103-3.4×2011=-6734.4…(6分)
∴
=3.4x-6734.4,
∵b>0
∴售房套数与年份成正相关关系…(8分)
(2)x=2014时,y=3.4x-6734.4=3.4×2014-6734.4=113.2
∴预测2014年小刚可能售出的房屋套数为113. …(12分)
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
∴b=
| (-2)(-6)+(-1)(-5)+0×0+1×5+2×6 |
| (-2)2+12+02+12+22 |
a=103-3.4×2011=-6734.4…(6分)
∴
 |
| y |
∵b>0
∴售房套数与年份成正相关关系…(8分)
(2)x=2014时,y=3.4x-6734.4=3.4×2014-6734.4=113.2
∴预测2014年小刚可能售出的房屋套数为113. …(12分)
点评:解决线性回归直线的方程,利用最小二乘法求出直线的截距和斜率,利用回归直线方程可预测.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对一切实数x,所有的二次函数f(x)=ax2+bx+c(a<b)的值均为非负实数,则
的最大值是( )
| b-a |
| a+b+c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
函数f(x)=
定义域是( )
| 1 | ||
|
| A、{x|x>5} |
| B、{x|x<5} |
| C、{x|x≥5} |
| D、{x|x≠5} |
不等式组
表示的区域的面积为( )
|
| A、2 | B、4 | C、6 | D、8 |

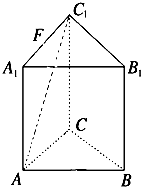 正三棱柱ABC-A1B1C1中底面边长为a,侧棱长为
正三棱柱ABC-A1B1C1中底面边长为a,侧棱长为