题目内容
(1)若关于x的不等式(ax-
)(x+4)≥0的解集为[-4,4],求实数a的值;
(2)若关于x的不等式ax2+bx+c>0的解集为(-1,2),求关于x的不等式
≥b的解集.
| 1 |
| a |
(2)若关于x的不等式ax2+bx+c>0的解集为(-1,2),求关于x的不等式
| a-c |
| x |
考点:一元二次不等式的解法,其他不等式的解法
专题:不等式的解法及应用
分析:(1)由题意可知:a<0.因此不等式(ax-
)(x+4)≥0可化为(x-
)(x+4)≤0,由于此不等式的解集为[-4,4],可得
=4,即可解出.
(2)由于关于x的不等式ax2+bx+c>0的解集为(-1,2),可知a<0,且-1,2是方程ax2+bx+c>0的两个实数根,利用根与系数的关系和一元二次不等式的解法即可得出.
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a2 |
(2)由于关于x的不等式ax2+bx+c>0的解集为(-1,2),可知a<0,且-1,2是方程ax2+bx+c>0的两个实数根,利用根与系数的关系和一元二次不等式的解法即可得出.
解答:
解:(1)由题意可知:a<0.∴不等式(ax-
)(x+4)≥0可化为(x-
)(x+4)≤0,
∵此不等式的解集为[-4,4],∴-4≤x≤
,
∴
=4,又a<0,解得a=-
.
(2)∵关于x的不等式ax2+bx+c>0的解集为(-1,2),∴a<0,且-1,2是方程ax2+bx+c>0的两个实数根,
∴
,化为b=-a,c=-2a.
不等式
≥b化为
≥-a,
∵a<0,∴
≤-1,即
≤0,
化为x(x+3)≤0,解得-3≤x≤0.
∴关于x的不等式
≥b的解集是{x|-3≤x≤0}.
| 1 |
| a |
| 1 |
| a2 |
∵此不等式的解集为[-4,4],∴-4≤x≤
| 1 |
| a2 |
∴
| 1 |
| a2 |
| 1 |
| 2 |
(2)∵关于x的不等式ax2+bx+c>0的解集为(-1,2),∴a<0,且-1,2是方程ax2+bx+c>0的两个实数根,
∴
|
不等式
| a-c |
| x |
| 3a |
| x |
∵a<0,∴
| 3 |
| x |
| 3+x |
| x |
化为x(x+3)≤0,解得-3≤x≤0.
∴关于x的不等式
| a-c |
| x |
点评:本题考查了一元二次方程的根与系数的关系和一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图,设四棱锥S-ACDE的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=
如图,设四棱锥S-ACDE的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=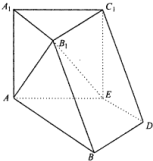 如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.