题目内容
已知四棱锥ABCD中,E、H、F、G分别是边AB、AD、BC、CD的中点.
(1)求证:BC与AD是异面直线;
(2)求证:EG与FH相交.
(1)求证:BC与AD是异面直线;
(2)求证:EG与FH相交.
考点:异面直线的判定,平面的基本性质及推论
专题:空间位置关系与距离
分析:(1)如图所示,由于BC?平面BCD,A∉平面BCD,D∈平面BCD,即可证明.
(2)E、H、F、G分别是边AB、AD、BC、CD的中点.由三角形的中位线定理可得:EH
FG,因此四边形EHGF是平行四边形.即可证明.
(2)E、H、F、G分别是边AB、AD、BC、CD的中点.由三角形的中位线定理可得:EH
| ∥ |
. |
解答:
证明:(1)如图所示,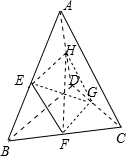
∵BC?平面BCD,A∉平面BCD,D∈平面BCD,
∴BC与AD是异面直线.
(2)∵E、H、F、G分别是边AB、AD、BC、CD的中点.
由三角形的中位线定理可得:EH
BD,FG
BD,
∴EH
FG,
∴四边形EHGF是平行四边形.
∴EG与FH相交.

∵BC?平面BCD,A∉平面BCD,D∈平面BCD,
∴BC与AD是异面直线.
(2)∵E、H、F、G分别是边AB、AD、BC、CD的中点.
由三角形的中位线定理可得:EH
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴EH
| ∥ |
. |
∴四边形EHGF是平行四边形.
∴EG与FH相交.
点评:本题考查了异面直线的判定方法、三角形的中位线定理、平行四边形的判定,考查了推理能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
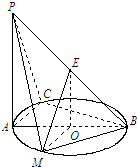 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.