题目内容
已知点A（-1，m）在抛物线C：y2=4x的准线上，过点A的直线与C在第一象限相切于点B，记C的焦点为F，若直线BF的斜率为
，则m=（ ）
| 4 |
| 3 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由抛物线的方程设切点B的坐标是（
，y0），并求出焦点F的坐标，由条件和斜率公式求出y0的值，再求出B的坐标，由点斜式方程设出切线的方程，联立抛物线的方程消去x后，由相切的条件：△=0求出斜率k的值，再求出切线方程，把点A的坐标代入求出m的值．
| y02 |
| 4 |
解答：
解：由题意设切点B的坐标是（
，y0），且y0＞0，
因为抛物线C：y2=4x的焦点F是（1，0），且直线BF的斜率为
，
所以
=
，化简得y02-3y0-4=0，
解得y0=4或y0=-1（舍去），
则B点的坐标是（4，4），
设过点A的切线方程是y-4=k（x-4），即y=kx-4k+4，
由
得，
y2-y-4k+4=0，
所以△=1-4×
×(-4k+4)=0，
化简得4k2-4k+1=0，解得k=
，
代入切线方程y=kx-4k+4得，y=
x+2，
把点A（-1，m）代入y=
x+2，解得m=
，
故选：D．
| y02 |
| 4 |
因为抛物线C：y2=4x的焦点F是（1，0），且直线BF的斜率为
| 4 |
| 3 |
所以
| y0-0 | ||
|
| 4 |
| 3 |
解得y0=4或y0=-1（舍去），
则B点的坐标是（4，4），
设过点A的切线方程是y-4=k（x-4），即y=kx-4k+4，
由
|
| k |
| 4 |
所以△=1-4×
| k |
| 4 |
化简得4k2-4k+1=0，解得k=
| 1 |
| 2 |
代入切线方程y=kx-4k+4得，y=
| 1 |
| 2 |
把点A（-1，m）代入y=
| 1 |
| 2 |
| 3 |
| 2 |
故选：D．
点评：本题考查抛物线的简单性质，直线的点斜式方程、斜率公式，以及直线与圆锥曲线的关系．
练习册系列答案
名校课堂系列答案
相关题目
下列函数中，既是奇函数又是增函数的是（ ）
| A、y=-x |
| B、y=x3+1 |
| C、y=sinx |
| D、y=x|x| |
已知集合A={x|x2+2x-3＜0}，B={x|-
＜x＜1}，则A∩B=（ ）
| 2 |
| A、∅ | ||
| B、{x|-3＜x＜1} | ||
C、{x|-
| ||
| D、A |
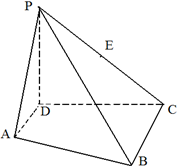如图，已知PD⊥平面ABCD，AD⊥CD，AD∥BC，PD=DC=BC；
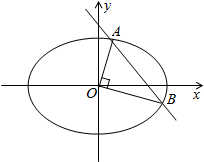已知焦点在x轴上的椭圆
如图，某三棱柱的正视图中的实线部分是边长为4的正方形，俯视图是等边三角形，则该三棱柱的侧视图的面积为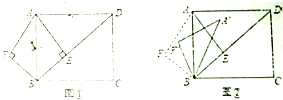
已知：如图①，在矩形ABCD中，AB=5，AD=