题目内容
13.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,已知$\sum_{i=1}^{10}$xi=225,$\sum_{i=1}^{10}$yi=1600,$\stackrel{∧}{b}$=4,该班某学生的脚长为24,据此估计其身高为( )| A. | 160 | B. | 163 | C. | 166 | D. | 170 |
分析 由数据求得样本中心点,由回归直线方程必过样本中心点,代入即可求得$\widehat{a}$,将x=24代入回归直线方程即可估计其身高.
解答 解:由线性回归方程为$\widehat{y}$=4x+$\widehat{a}$,
则$\overline{x}$=$\frac{1}{10}$$\sum_{i=1}^{10}$xi=22.5,$\overline{y}$=$\frac{1}{10}$$\sum_{i=1}^{10}$yi=160,
则数据的样本中心点(22.5,160),
由回归直线方程样本中心点,则$\widehat{a}$=$\widehat{y}$-4x=160-4×22.5=70,
∴回归直线方程为$\widehat{y}$=4x+70,
当x=24时,$\widehat{y}$=4×24+70=166,
则估计其身高为166,
故选C.
点评 本题考查回归直线方程的求法及回归直线方程的应用,考查计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知函数f(x)=sin(ωx+φ)(φ>0,-π<φ<0)的最小正周期是π,将f(x)图象向左平移$\frac{π}{3}$个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
| A. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | B. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递减 | D. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增 |
8.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如图:
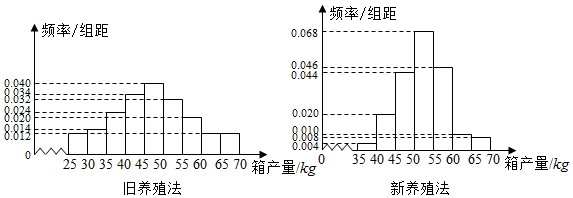
(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
| 箱产量<50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
18.已知当x∈[0,1]时,函数y=(mx-1)2 的图象与y=$\sqrt{x}$+m的图象有且只有一个交点,则正实数m的取值范围是( )
| A. | (0,1]∪[2$\sqrt{3}$,+∞) | B. | (0,1]∪[3,+∞) | C. | (0,$\sqrt{2}$)∪[2$\sqrt{3}$,+∞) | D. | (0,$\sqrt{2}$]∪[3,+∞) |
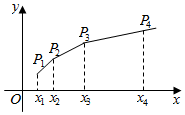 已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.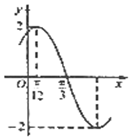 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,下列说法正确的有( )个
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,下列说法正确的有( )个