题目内容
11．已知F是抛物线C：y2=8x的焦点，M是C上一点，FM的延长线交y轴于点N．若M为FN的中点，则|FN|=6．分析 求出抛物线的焦点坐标，推出M坐标，然后求解即可．
解答 解：抛物线C：y2=8x的焦点F（2，0），M是C上一点，FM的延长线交y轴于点N．若M为FN的中点，
可知M的横坐标为：1，则M的纵坐标为：$±2\sqrt{2}$，
|FN|=2|FM|=2$\sqrt{（1-2）^{2}+（±2\sqrt{2}-0）^{2}}$=6．
故答案为：6．
点评 本题考查抛物线的简单性质的应用，考查计算能力．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
1．海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如下：
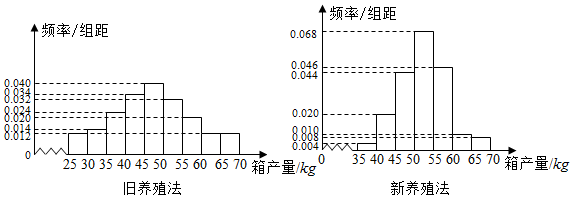
（1）记A表示事件“旧养殖法的箱产量低于50kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
（3）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较．
附：
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
（1）记A表示事件“旧养殖法的箱产量低于50kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
| 箱产量＜50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
附：
| P（K2≥K） | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
2．已知sinα-cosα=$\frac{4}{3}$，则sin2α=（ ）
| A． | -$\frac{7}{9}$ | B． | -$\frac{2}{9}$ | C． | $\frac{2}{9}$ | D． | $\frac{7}{9}$ |
6．已知直三棱柱ABC-A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{15}}{5}$ | C． | $\frac{\sqrt{10}}{5}$ | D． | $\frac{\sqrt{3}}{3}$ |
16．甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（ ）
| A． | 乙可以知道四人的成绩 | B． | 丁可以知道四人的成绩 | ||
| C． | 乙、丁可以知道对方的成绩 | D． | 乙、丁可以知道自己的成绩 |
4．已知函数f（x）=sin（ωx+φ）（φ＞0，-π＜φ＜0）的最小正周期是π，将f（x）图象向左平移$\frac{π}{3}$个单位长度后，所得的函数图象过点P（0，1），则函数f（x）（ ）
| A． | 在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上单调递减 | B． | 在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上单调递增 | ||
| C． | 在区间[-$\frac{π}{3}$，$\frac{π}{6}$]上单调递减 | D． | 在区间[-$\frac{π}{3}$，$\frac{π}{6}$]上单调递增 |
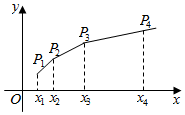已知{xn}是各项均为正数的等比数列，且x1+x2=3，x3-x2=2．