题目内容
8．直线l1：x-y+1=0，l2：x-y=0之间的距离为（ ）| A． | 1 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
分析 把已知数据代入平行线间的距离公式，计算可得．
解答 解：∵直线l1：x-y+1=0，l2：x-y=0，
∴由平行线间的距离公式可得d=$\frac{|1-0|}{\sqrt{{1}^{2}+（-1）^{2}}}$=$\frac{\sqrt{2}}{2}$，
故选：B．
点评 本题考查平行线间的距离公式，属基础题．
练习册系列答案
相关题目
18．已知圆C：x2+y2=1，点P在直线l：y=x+2上，若圆C上存在两点A，B使得$\overrightarrow{PA}=3\overrightarrow{PB}$，则点P的横坐标的取值范围为（ ）
| A． | $[{-1，\frac{1}{2}}]$ | B． | $[{-2，\frac{1}{2}}]$ | C． | [-1，0] | D． | [-2，0] |
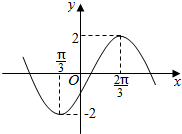已知函数f（x）=Asin（ωx+φ）（其中A，ω，φ为常数，且A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示：
如图，在正三棱柱ABC-A1B1C1中，D是边BC上异于C的一点，AD⊥C1D．
如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别是AB，AD的中点，过EF的截面EFG与底面成60°二面角，且与棱AA1交于G，求棱锥G-AEF的体积．