题目内容
13．函数f（x）=x3-3x2+m在区间[-1，1]上的最大值是2，则常数m=（ ）| A． | -2 | B． | 0 | C． | 2 | D． | 4 |
分析 求出函数的导数，得到函数的单调区间，求出函数的最大值是f（0）=m，则m值可求．
解答 解：f′（x）=3x（x-2），
令f′（x）＞0，解得：x＞2或x＜0，
令f′（x）＜0，解得：0＜x＜2，
∴f（x）在[-1，0）递增，在（0，1]递减，
∴f（x）max=f（0）=m=2，
故选：C．
点评 本题考查利用导数求函数在闭区间上的最值，考查了导数的综合应用，属于基础题．
练习册系列答案
相关题目
8．已知集合A={x|y=lnx}，B={-2，-1，1，2}，则A∩B=（ ）
| A． | {-1，-2} | B． | {1，2} | C． | （0，+∞） | D． | （1，2） |
5．已知圆锥的表面积等于12πcm2，其侧面展开图是一个半圆，则底面圆的半径为（ ）
| A． | 1cm | B． | 2cm | C． | 3cm | D． | $\frac{3}{2}cm$ |
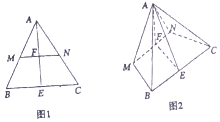已知在边长为4的等边△ABC（如图1所示）中，MN∥BC，E为BC的中点，连接AE交MN于点F，现将△AMN沿MN折起，使得平面AMN⊥平面MNCB（如图2所示）．
3．已知A（2，0），B（3，$-\sqrt{3}$），直线 l∥AB，则直线l的倾斜角为（ ）
| A． | 135° | B． | 120° | C． | 60° | D． | 45° |