题目内容
3．双曲线2x2-y2=16的实轴长等于4$\sqrt{2}$．分析 化简双曲线方程方程为标准方程，然后求解实轴长即可．
解答 解：双曲线2x2-y2=16的标准方程：$\frac{{x}^{2}}{8}-\frac{{y}^{2}}{16}=1$，
可得a=2$\sqrt{2}$．
双曲线2x2-y2=16的实轴长等于：4$\sqrt{2}$．
故答案为：$4\sqrt{2}$．
点评 本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
2．已知双曲线M的实轴长为2，且它的一条渐近线方程为y=2x，则双曲线M的标准方程可能是（ ）
| A． | x2-4y2=1 | B． | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1 | C． | $\frac{{y}^{2}}{4}$-x2=1 | D． | y2-4x2=1 |
8．已知集合A={-$\frac{1}{3}$，$\frac{1}{2}$}，B={x|ax+1=0}}，且B⊆A，则a的可取值组成的集合为（ ）
| A． | {-3，2} | B． | {-3，0，2} | C． | {3，-2} | D． | {3，0，-2} |
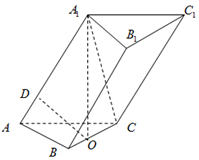三棱柱ABC-A1B1C1的底面ABC是等边三角形，BC的中点为O，A1O⊥底面ABC，AA1与底面ABC所成的角为$\frac{π}{3}$，点D在棱AA1上，且AD=$\sqrt{3}$，AB=4．