题目内容
12.在正方体ABCD-A1B1C1D1中,底面ABCD是边长为3$\sqrt{2}$的正方形,AA1=3,E是线段A1B1上一点,若二面角A-BD-E的正切值为3,则三棱锥A-A1D1E外接球的表面积为35π.分析 过E作EF∥AA1.交AB与F,过F作FG⊥DB于G,则∠EGF就是二面角A-BD-E的平面角,由tan∠EGF=3,可得FG=1,求出三棱锥A-A1D1E外接球的直径即可
解答 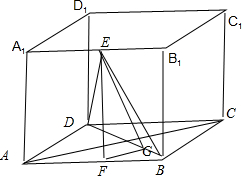 解:过E作EF∥AA1.交AB与F,过F作FG⊥DB于G,
解:过E作EF∥AA1.交AB与F,过F作FG⊥DB于G,
则∠EGF就是二面角A-BD-E的平面角,∵tan∠EGF=$\frac{EF}{FG}=3$,
∴FG=1,则BF=$\sqrt{2}$,∴$AF=2\sqrt{2}$,
∴三棱锥A-A1D1E外接球的直径为$\sqrt{8+9+18}=\sqrt{35}$,
∴外接球的表面积为35π.
故答案为:35π.
点评 本题考查了三棱锥的外接球的表面积,关键是找到动点位置,求出半径,属于中档题.

练习册系列答案
相关题目
20.函数g(x)=ax3+2(1-a)x2-3ax在区间(-∞,$\frac{a}{3}$)内单调递减,则a的取值范围为( )
| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | -1≤a≤0 |
17.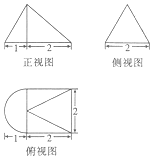 某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )
某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )
 某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )
某几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的表面积为( )| A. | $\frac{(8+π)\sqrt{3}}{2}$ | B. | $\frac{(8+π)\sqrt{3}}{6}$ | C. | $\frac{π}{2}$+4+$\frac{5}{2}$$\sqrt{3}$ | D. | $\frac{3}{2}$π+8+$\sqrt{7}$ |
4.已知集合$A=\{x|{(\frac{1}{2})^x}≤1\}$,B={x|x2-2x-8≤0},则A∩B=( )
| A. | {x|-2≤x≤0} | B. | {x|2≤x≤4} | C. | {x|0≤x≤4} | D. | {x|x≤-2} |