题目内容
14.若E,F,G分别为正三角形ABC的边AB,BC,CA的中点,以△EFG为底面,把△AEG,△BEF,△CFG折起使A,B,C重合为一点P,则下列关于线段PE与FG的论述不正确的为( )| A. | 垂直 | B. | 长度相等 | C. | 异面 | D. | 夹角为60° |
分析 由题意三棱锥P-EFG为正四面体,则线段PE与FG长度相等且异面垂直,即可得出结论.
解答 解:由题意三棱锥P-EFG为正四面体,则线段PE与FG长度相等且异面垂直,
故选D.
点评 本题考查正四面体的性质,考查平面图形的翻折,比较基础.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
4.已知sinα+cosα=$\frac{\sqrt{3}}{2}$,且α∈(0,π),则sin2α的值为( )
| A. | -$\frac{\sqrt{15}}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | $\frac{1}{4}$ |
5.设f(x)=$\left\{\begin{array}{l}{x+1,(x>0)}\\{π,(x=0)}\\{0,(x<0)}\end{array}\right.$,则f(f(f(-1)))=( )
| A. | 0 | B. | π+1 | C. | π | D. | -1 |
9.过两点A(2,1)和B(3,m)直线的斜率为1,则实数m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.化3$\sqrt{3\sqrt{3\sqrt{3}}}$为分数指数幂结果是( )
| A. | 3${\;}^{\frac{7}{8}}$ | B. | 3${\;}^{\frac{15}{8}}$ | C. | 3${\;}^{\frac{7}{4}}$ | D. | 3${\;}^{\frac{17}{8}}$ |
4.若等差数列{an}满足a1+a2+a2015+a2016=3,则{an}的前2016项之和S2016=( )
| A. | 1506 | B. | 1508 | C. | 1510 | D. | 1512 |
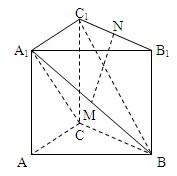 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.