数列{an}的通项公式an=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$.则它的前8项和S8=2．题目和参考答案——青夏教育精英家教网——

题目内容

16．数列{a_n}的通项公式a_n=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$，则它的前8项和S₈=2．

分析通过裂项可知a_n=$\sqrt{n+1}$-$\sqrt{n}$，进而并项相加即得结论．

解答解：∵a_n=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$，
∴数列{a_n}的前8项和S₈=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{9}$-$\sqrt{8}$=$\sqrt{9}$-1=2，
故答案为：2．

点评本题考查数列的通项及前n项和，裂项是解决本题的关键，注意解题方法的积累，属于基础题．

练习册系列答案

红领巾乐园系列答案

初中英语最佳方案冲刺AB卷系列答案

新中考指南系列答案

快乐起跑线期末冲刺系列答案

快乐起跑线周考卷系列答案

快乐起跑线单元滚动活页测系列答案

快乐学习一点通系列答案

智慧翔课时导学案系列答案

随堂演练系列答案

中考一本通系列答案

相关题目

6．设a=sin33°，b=cos55°，c=tan35°，d=log₃5，则a，b，c，d按从大到小的顺序是d＞c＞b＞a．

7．某班级有50名学生，现用系统抽样的方法从这50名学生中抽出10名学生，将这50名学生随机编号为1～50号，并按编号顺序平均分成10组（1～5号，6～10号，…，46～50号），若在第三组抽到的编号是13，则在第七组抽到的编号是（　　）

4．若经过点$（{4，\sqrt{3}}）$的双曲线的渐近线方程为$y=\frac{1}{2}x$，则双曲线的标准方程为$\frac{x^2}{4}-{y^2}=1$．

11．已知数列{a_n}的前n项和为S_n，且满足a₁=1，a_n+1=S_n+1（n∈N⁺）
（1）求{a_n}的通项公式；
（2）数列{b_n}是等差数列，前n项和为T_n，若T₃=30，b_n≥0（n∈N⁺）且a₁+b₁，a₂+b₂，a₃+b₃成等比数列，求T_n．
（3）证明：$\frac{{T}_{n}}{{a}_{n}}$≤9（n∈N⁺）

1．利用加、减、乘、除、指数、对数、阶乘等运算，将3个3组合起来，写出一个式子，使得式子的运算结果分别为1，2，3，4等，例如（$\frac{3}{3}$）³=1，$\frac{3+3}{3}$=2，3+log₃3=4，请写出三个类似式子，使得运算结果分别为：3，5，6；3+3-3=3，3+3！÷3=5，3×3-3=6．

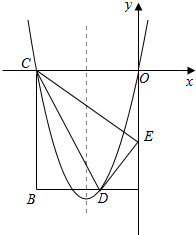如图，在矩形ABCD中，OA=5，AB=4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B恰好落在OA上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．
（1）求OE的长及经过O，D，C三点抛物线的解析式；
（2）一动点P从点C出发，沿CB以每秒2个单位长度的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长度的速度向点C运动，当点P到达点B时，两点同时停止运动，设运动时间为t秒，当t为何值时，DP=DQ；
（3）若点N在（1）中抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点坐标；若不存在，请说明理由．

5．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，且|$\overline{a}$|=1，|$\overrightarrow{b}$|=2，若$\overrightarrow{a}$-2$\overrightarrow{b}$与k$\overrightarrow{a}$+$\overrightarrow{b}$互相垂直，则实数k的值为3．

6．若x＞0，则函数y=-x-$\frac{1}{x}$（　　）