题目内容
18.过点P(2,4)引圆(x-1)2+(y-1)2=1的切线,则切线方程为x=2或4x-3y+4=0.分析 当切线方程斜率不存在时,直线x=2满足题意;当切线方程斜率存在时,设出切线方程,根据圆心到切线的距离d=r列出关于k的方程,求出方程的解得到k的值,确定出此时切线方程,综上,得到满足题意的切线方程.
解答 解:分两种情况考虑:
若切线方程斜率不存在时,直线x=2满足题意;
若切线方程斜率存在时,设为k,此时切线方程为y-4=k(x-2),即kx-y+4-2k=0,
∵直线与圆相切,∴圆心(1,1)到切线的距离d=r,即$\frac{|k-1+4-2k|}{\sqrt{{k}^{2}+1}}$=1,
解得:k=$\frac{4}{3}$,此时切线方程为4x-3y+4=0,
综上,切线方程为x=2或4x-3y+4=0.
故答案为:x=2或4x-3y+4=0.
点评 此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,直线的点斜式方程,利用了分类讨论的思想,分类讨论时注意考虑问题要全面,做到不重不漏.

练习册系列答案
相关题目
9.已知公比为q的等比数列{an},且满足条件|q|>1,a2+a7=2,a4a5=-15,则a12=( )
| A. | -$\frac{27}{25}$ | B. | -$\frac{25}{3}$ | C. | -$\frac{27}{25}$或-$\frac{25}{3}$ | D. | $\frac{25}{3}$ |
6.已知向量$\overrightarrow{a}$=(1,2),则|$\overrightarrow{a}$|=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,PA=BC=AC=4,D为PC的中点.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,PA=BC=AC=4,D为PC的中点.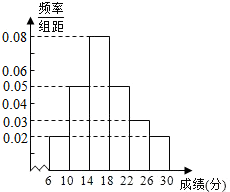 某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.