题目内容
已知在平面直角坐标系xOy中,曲线E的参数方程为
(θ为参数),以原点作为极点,x轴的正半轴为极轴建立极坐标系且单位长度相同,直线L过极轴上一点M(2,0)且L向上的方向与极轴的正方向成
π.
(1)写出L的极坐标方程;
(2)求直线L被曲线E截得的弦长.
|
| 5 |
| 6 |
(1)写出L的极坐标方程;
(2)求直线L被曲线E截得的弦长.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)由于直线L过极轴上一点M(2,0)且L向上的方向与极轴的正方向成
π.可得直角坐标方程为,把
代入可得L的极坐标方程.
(2)曲线E的参数方程为
(θ为参数),化为(x-
)2+(y-1)2=9,可得圆心E(
,1),半径r=3.利用点到直线的距离公式可得圆心E到直线L的距离d.即可得出直线L被曲线E截得的弦长=2
.
| 5 |
| 6 |
|
(2)曲线E的参数方程为
|
| 3 |
| 3 |
| r2-d2 |
解答:
解:(1)∵直线L过极轴上一点M(2,0)且L向上的方向与极轴的正方向成
π.
∴直角坐标方程为;y=tan
(x-2),化为x+
y-2=0,
把
代入可得ρcosθ+
ρsinθ-2=0,即为L的极坐标方程.
(2)曲线E的参数方程为
(θ为参数),化为(x-
)2+(y-1)2=9,
可得圆心E(
,1),半径r=3.
∴圆心E到直线L的距离d=
=
-1.
∴直线L被曲线E截得的弦长=2
=2
=2
.
| 5 |
| 6 |
∴直角坐标方程为;y=tan
| 5π |
| 6 |
| 3 |
把
|
| 3 |
(2)曲线E的参数方程为
|
| 3 |
可得圆心E(
| 3 |
∴圆心E到直线L的距离d=
|
| ||||
|
| 3 |
∴直线L被曲线E截得的弦长=2
| r2-d2 |
32-(
|
5+2
|
点评:本题考查了极坐标方程与直角坐标方程的互化、直线与圆的相交弦长问题、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=x+y( )
|
| A、有最小值-3,最大值2 |
| B、有最小值1,无最大值 |
| C、有最大值2,无最小值 |
| D、既无最小值,也无最大值 |
某程序框图如图所示,则输出的结果S=( )
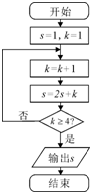

| A、11 | B、26 | C、57 | D、120 |
不等式(x+1)(2-x)>0的解集是( )
| A、(-2,1) |
| B、(-1,2) |
| C、(-∞,-2)∪(1,+∞) |
| D、(-∞,-1)∪(2,+∞) |
